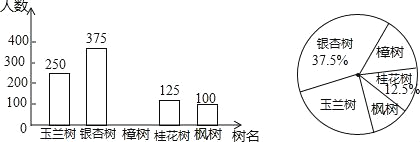
��Ŀ����
����Ŀ����֪������y��ax2+bx+3������A����1��0����B��3��0��������y�ύ�ڵ�C�������ߵĶԳ�����x�ύ�ڵ�D��
(1)�������ߵĽ���ʽ��
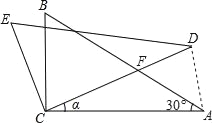
(2)��P��y���������ϵ�һ�����㣬����DP�����߶�DP���ŵ�D˳ʱ����ת90���õ��߶�DE����P�Ķ�Ӧ��Eǡ�������������ϣ������ʱ��P�����ꣻ
(3)��M��m��n�����������ϵ�һ�����㣬����MD����MD2��ʾ���Ա���n�ĺ����������MD2ȡ����Сֵʱ��M�����꣮
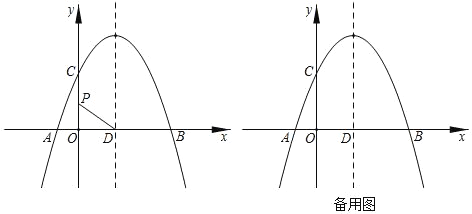
���𰸡���1��y����x2+2x+3����2����P������Ϊ��0��1+![]() ������3��MD2��n2��n+4����M������Ϊ��
������3��MD2��n2��n+4����M��������![]() ��
��![]() ������
������![]() ��
��![]() ����
����
��������
��1�����ݵ�A��B�����꣬���ô���ϵ����������������ߵĽ���ʽ����2������E��EF��x���ڵ�F��������ת�����ʼ�ͬ�ǵ������ȣ���֤����ODP�ա�FED��AAS�����������ߵĽ���ʽ�ɵó���D�����꣬�����ɵó�OD�ij��ȣ�����ȫ�������ε����ʿɵó�EF�ij��ȣ������ö��κ���ͼ���ϵ���������������DF��OP�ij�����ϵ�P��y�������ἴ�ɵó���P�����ꣻ��3�����ö��κ���ͼ���ϵ�����������ɵó�m2��2m��3��n�����ݵ�D��M�����꣬���������ľ��빫ʽ�ɵó�MD2��n2��n+4�������䷽���ɵó���MD2ȡ����Сֵʱn��ֵ�������ö��κ���ͼ���ϵ�������������������MD2ȡ����Сֵʱ��M�����꣮
��1����A����1��0����B��3��0������y��ax2+bx+3���ã�![]() ��
��
��ã�![]() ��
��
�������ߵĽ���ʽΪy����x2+2x+3��
��2������E��EF��x���ڵ�F����ͼ��ʾ��
�ߡ�OPD+��ODP��90�㣬��ODP+��FDE��90�㣬
���OPD����FDE��
�ڡ�ODP�͡�FED�У�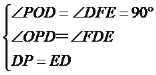 ��
��
���ODP�ա�FED��AAS����
��DF��OP��EF��DO��
�������ߵĽ���ʽΪy����x2+2x+3������x��1��2+4��
���D��������1��0����
��EF��DO��1��
��y��1ʱ����x2+2x+3��1��
��ã�x1��1��![]() ����ȥ����x2��1+
����ȥ����x2��1+![]() ��
��
��DF��OP��1+![]() ��
��
���P��������0��1+![]() ����
����
��3���ߵ�M��m��n�����������ϵ�һ�����㣬
��n����m2+2m+3��
��m2��2m��3��n��
�ߵ�D������Ϊ��1��0����
��MD2����m��1��2+��n��0��2��m2��2m+1+n2��3��n+1+n2��n2��n+4��
��n2��n+4����n��![]() ��2+
��2+![]() ��
��
�൱n��![]() ʱ��MD2ȡ����Сֵ����ʱ��m2+2m+3��
ʱ��MD2ȡ����Сֵ����ʱ��m2+2m+3��![]() ��
��
��ã�m1��![]() ��m2��
��m2��![]() ��
��
��MD2��n2��n+4��
��MD2ȡ����Сֵʱ����M������Ϊ��![]() ��
��![]() ����
����![]() ��
��![]() ����
����