Question

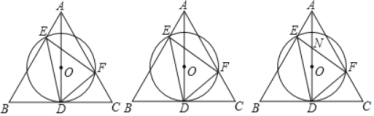
【题目】如图：AD是正△ABC的高，O是AD上一点，⊙O经过点D，分别交AB、AC于E、F

（1）求∠EDF的度数；

（2）若AD＝6，求△AEF的周长；

（3）设EF、AD相较于N，若AE＝3，EF＝7，求DN的长．

Answer 1

【答案】（1）60°；⑵18；⑶DN=

【解析】

（1）作OI⊥AB于I，OJ⊥AC于J，连接OE，OF，可得△OIE≌△OJF（HL），∠EOF=120°，

可得∠EDF的度数；

（2）设AD与圆O交于点G，连接FG，AD是正△ABC的高，∠B=∠C=60°，CD=BD， GD是圆O的直径,由圆与正三角形的对称性，可得∠BED=∠ FED， 作DK⊥AB，DL⊥AC，DM⊥EF，可得DK=DL，可得△EKD≌EFD与△DMF≌△DLF，可得△AEF的周长=AF+AE+EF=2AL，可得答案.

（3）过E点AC的垂线，长为，过E点做AD的垂线，长为，过F做AD的垂线，长为,设AC=x，==，AF=-10,FC=10-,EB=x-3,BD=DC=,由△FDC∽△DEB，可得，代入可得x的值，由=，可得AN，可求得DN.

解：（1）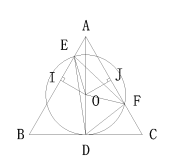

AD是正△ABC的高，∴∠BAC=60°，AD平分∠BAC，

∴∠BAD=∠CAD=30°，

作OI⊥AB于I，OJ⊥AC于J，连接OE，OF，∴OI=OJ，

∴△OIE≌△OJF（HL），∴∠IOE=∠JOF

∴∠EOF=∠EOJ+∠FOJ=∠EOJ+∠IOE=∠IOJ=120°，

∴∠EDF=∠EOF=60°

⑵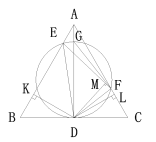

设AD与圆O交于点G，连接FG，AD是正△ABC的高，∠B=∠C=60°，CD=BD， GD是圆O的直径,由圆与正三角形的对称性，可得∠BED=∠ FED， 作DK⊥AB，DL⊥AC，DM⊥EF，可得DK=DL

∠BED=∠ FED，DK⊥AB， DM⊥EF，ED=ED

△EKD≌EFD, EK=EM,DK=DM,

在△DMF与△DLF中，

DK=DM=DL, DL⊥AC，DM⊥EF,

△DMF≌△DLF, MF=FL

易得：AK=AL,AL=AC=9

△AEF的周长=AF+AE+EF=2AL，AL=9，∴=18=

⑶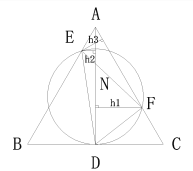

过E点AC的垂线，长为，过E点做AD的垂线，长为，过F做AD的垂线，长为,

设AC=x，==，AF=-10,FC=10-,EB=x-3,BD=DC=,

由△FDC∽△DEB，可得,代入得：

，解得：=12，=（舍去），

AF=-10=8,AD==,

=

可得AN=

DN=