题目内容
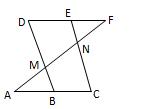
如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC =70°.
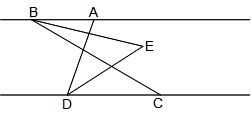
(1)求∠EDC的度数;
(2)若∠ABC =n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移, 使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示),不改变,请说明理由.
解:(1)∵DE平分∠ADC,∠ADC=70°,∴∠EDC= ∠ADC=
∠ADC= ×70°=35°;
×70°=35°;
(2)过点E作EF∥AB,

∵AB∥CD, ∴AB∥CD∥EF, ∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠A BE=
BE= ∠ABC=
∠ABC= n°,∠CDE=
n°,∠CDE= ∠ADC=35°, ∴∠BED=∠BEF+∠DEF=
∠ADC=35°, ∴∠BED=∠BEF+∠DEF= n°+35°;
n°+35°;
(3)过点E作EF∥AB
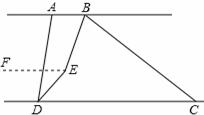
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70° ∴∠ABE= ∠ABC=
∠ABC= n°,∠CDE=
n°,∠CDE= ∠ADC=35°
∠ADC=35°
∵AB∥CD,∴AB∥CD∥EF, ∴∠BEF=180°-∠ABE=180°- n°,∠CDE=∠DEF=35°,
n°,∠CDE=∠DEF=35°,
∴∠BED=∠BEF+∠DEF=180°- n°+35°=215°-
n°+35°=215°- n°.
n°.
故∠BED的度数发生了改为,改变为(215- n)°.
n)°.
【难度】困难

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
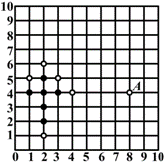
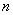 (岁)满足关系式:
(岁)满足关系式: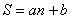 ,其中
,其中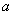 、
、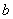 均为常数.
均为常数.

 ,其中
,其中 .
.
 ,A与
,A与