题目内容
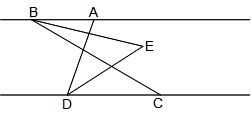
如图，已知AB∥CD，∠BED=90°，那么∠B＋∠D等于多少度？为什么？
解：过点E作EF∥AB，
得∠B＋∠BEF=180°（ 两直线平行，同旁内角互补），
因为AB∥CD（已知），
EF∥AB（所作），
所以EF∥CD（平行的传递性）．
得∠DEF+∠D=180°（两直线平行，同旁内角互补），
所以∠B＋∠BEF＋∠DEF＋∠D=360°（等式性质）．
即∠B+∠BED+∠D =360°．
因为∠BED=90°（已知），
所以∠B＋∠D=270°（等式性质）．
练习册系列答案
相关题目
之间的一动点，当点P运动到某一位置时，连接PA，PB．
，求x＋y的值．
