题目内容
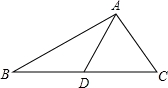
如图,点D为码头,A,B两个灯塔与码头的距离相等,DA,DB为海岸线.一轮船离开码头,计划沿∠ADB的角平分线航行,在航行途中C点处,测得轮船与灯塔A和灯塔B的距离相等.试问:轮船航行是否偏离指定航线?请说明理由.
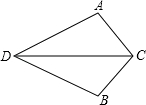
【考点】全等三角形的应用.
【分析】只要证明轮船与D点的连线平分∠ADB就说明轮船没有偏离航线,也就是证明∠ADC=∠BDC,证角相等,常常通过把角放到两个三角形中,利用题目条件证明这两个三角形全等,从而得出对应角相等.
【解答】解:此时轮船没有偏离航线.
理由:由题意知:DA=DB,AC=BC,
在△ADC和△BDC中,
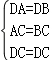 ,
,
∴△ADC≌△BDC(SSS),
∴∠ADC=∠BDC,
即DC为∠ADB的角平分线,
∴此时轮船没有偏离航线.
【点评】本题考查了全等三角形的应用,解答本题的关键是:根据条件设计三角形全等,巧妙地借助两个三角形全等,寻找对 应角相等.要学会把实际问题转化为数学问题来解决.
应角相等.要学会把实际问题转化为数学问题来解决.

练习册系列答案
相关题目
 有增根,则m的值为__________.
有增根,则m的值为__________. ﹣
﹣ =0
=0 
 ,
, ,
, ,﹣2,0,1.020020002…(相邻两个2之间0的个数逐次加1),其中无理数有( )
,﹣2,0,1.020020002…(相邻两个2之间0的个数逐次加1),其中无理数有( )