题目内容
如图，这是两块相同的三角板拼成的一个图形，BC边与DF边在同一条直线上．请找出图中的一组平行线，并说明你的理由．考点：平行线的判定
专题：
分析：根据三角板可得∠B=∠EDC=60°，再根据同位角相等两直线平行可得AB∥DE．
解答：解：AB∥DE，
理由：∵∠B=∠EDC=60°，
∴AB∥DE．
理由：∵∠B=∠EDC=60°，
∴AB∥DE．
点评：此题主要考查了平行线的判定，关键是掌握同位角相等两直线平行．
练习册系列答案
相关题目
从n个苹果和4个雪梨中，任选1个，若选中苹果的概率是
，则n的值是（ ）
| 1 |
| 2 |
| A、4 | B、3 | C、2 | D、1 |
小马虎在计算16-
x时，不慎将“-”看成了“+”，计算的结果是17，那么正确的计算结果应该是（ ）
| 1 |
| 3 |
| A、15 | B、13 | C、7 | D、-1 |
如图，已知A、B、C为⊙O上的三点，∠BAC=30°，则∠BOC等于（ ）| A、30° | B、40° |
| C、50° | D、60° |
下列几何图形或函数图象中，不一定是轴对称图形的是（ ）
| A、圆 | B、二次函数图象 |
| C、反比例函数图象 | D、直角三角形 |
如图图案中既是轴对称图形又是中心对称图形的是（ ）
A、 |
B、 |
C、 |
D、 |
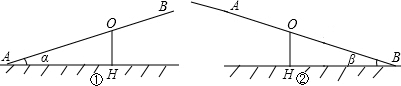
已知跷跷板AB长3m，由于跷跷板的支撑点O偏离中点，所以当A端碰到地面时，AB与地面的夹角为α（如图①），当B端碰到地面时，AB与地面的夹角为β（如图②），则跷跷板AB的支撑点O到地面的高度OH用含α、β的式子表示正确的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|