题目内容
15.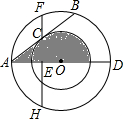 以O为圆心的两个同心圆中,AD是大圆的直径,大圆的弦AB与小圆相切于点C,过C点作FH⊥AD交大圆于F、H,垂足为E.
以O为圆心的两个同心圆中,AD是大圆的直径,大圆的弦AB与小圆相切于点C,过C点作FH⊥AD交大圆于F、H,垂足为E.(1)判断AC与BC的大小关系,并说明理由.
(2)如果FC、CH的长是方程x2-2$\sqrt{5}$x+4=0的两根(CH>CF),求CE、CA的长以及图中阴影部分的面积.
分析 (1)相等,主要根据是垂径定理,从已知条件中可知AB为大圆的弦,且垂直于半径,所以相等.
(2)先解方程求出根,再观察图发现阴影部分图形的周长就是一段弧长加一线段,分别计算相加.
解答  (1)解:相等.
(1)解:相等.
连接OC,则CO⊥AB,故AC=BC.
(2)解:解方程得:CH=$\sqrt{5}$+1,CF=$\sqrt{5}$-1,
∴CE=EF-FC=EH-FC=$\sqrt{5}$-($\sqrt{5}$-1)=1,AC2=4,AC=2,
在Rt△ACE中,sinA=$\frac{CE}{AC}$,
∴∠A=30°,
∴∠AOC=60°,
∴∠CON=120°.
在△ACO中,CO=AC•tanA=2×$\frac{\sqrt{3}}{3}$,
阴影部分的面积=S△ACO+S扇形=$\frac{1}{2}×2×\frac{2\sqrt{3}}{3}$+$\frac{120π×(\frac{2\sqrt{3}}{3})^{2}}{360}$=$\frac{2\sqrt{3}}{3}$+$\frac{4π}{9}$.
点评 本题考查了切线的性质,勾股定理,解直角三角形,垂径定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
10. 如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
 如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )| A. | 180° | B. | 360° | C. | 270° | D. | 540° |
4. 如图,一个高为1m的油筒内有油,一根木棒长1.2m,从桶盖小口斜插入桶内,一端到底部,另一端正好到小口,抽出木棒,量得棒上浸油部分的长0.36m,则桶内油的高度为( )
如图,一个高为1m的油筒内有油,一根木棒长1.2m,从桶盖小口斜插入桶内,一端到底部,另一端正好到小口,抽出木棒,量得棒上浸油部分的长0.36m,则桶内油的高度为( )
 如图,一个高为1m的油筒内有油,一根木棒长1.2m,从桶盖小口斜插入桶内,一端到底部,另一端正好到小口,抽出木棒,量得棒上浸油部分的长0.36m,则桶内油的高度为( )
如图,一个高为1m的油筒内有油,一根木棒长1.2m,从桶盖小口斜插入桶内,一端到底部,另一端正好到小口,抽出木棒,量得棒上浸油部分的长0.36m,则桶内油的高度为( )| A. | 0.28m | B. | 0.385m | C. | 0.4m | D. | 0.3m |
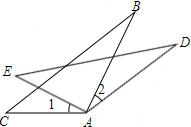 如图,AC=AE,AB=AD,∠1=∠2,求证:∠B=∠D.
如图,AC=AE,AB=AD,∠1=∠2,求证:∠B=∠D.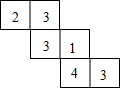 一个几何体由若干个大小相同的小立方块搭成,从上面看到的这个几何体的形状如图所示.其中小正方形中的数字表示在该位置小立方块的个数,请你画出从正面和从左面看到的这个几何体的形状图.
一个几何体由若干个大小相同的小立方块搭成,从上面看到的这个几何体的形状如图所示.其中小正方形中的数字表示在该位置小立方块的个数,请你画出从正面和从左面看到的这个几何体的形状图. 一辆火车从百货大楼出发负责送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.
一辆火车从百货大楼出发负责送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.