题目内容
12.观察下列按一定规律排列的图形:
(1)第5个图形、第6个图形、第9个图形中“★“的个数各是多少?
(2)如果按这一规律排列下去,第n个图形中“★”的个数又是多少?(用含有n的代数式表示);
(3)第2012个图形中“★”的个数又是多少?
分析 (1)观察图形发现每增加一个图形增加2个五星,由此得到规律求解;
(2)根据(1)写出通项公式,从而表示出规律;
(3)根据规律列式求解即可.
解答 解:观察发现每增加一个图形增加2个五星,
即:第1个图有4+2×0=4个五星;
第2个图有4+2×1=6个五星;
第3个图有4+2×2=8个五星;
…
第n个图有4+2×(n-1)=2n+2个五星;
(1)当n=5时,2×5+2=12;
当n=6时,2×6+2=14;
当n=9时,2×9+2=20个五星;
(2)2+2n或2(n+1);
(3)当n=2012时,2(n+1)=2×2013=4026(个).
点评 本题考查规律型中的图形变化问题,解决此类探究性问题,关键在观察、分析已知数据,寻找它们之间的相互联系,探寻其规律.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
2.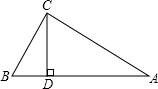 如图,在△ABC中,∠ACB=90°,∠A=30°,AB=2$\sqrt{5}$,CD是AB边上的高.则BD等于( )
如图,在△ABC中,∠ACB=90°,∠A=30°,AB=2$\sqrt{5}$,CD是AB边上的高.则BD等于( )
 如图,在△ABC中,∠ACB=90°,∠A=30°,AB=2$\sqrt{5}$,CD是AB边上的高.则BD等于( )
如图,在△ABC中,∠ACB=90°,∠A=30°,AB=2$\sqrt{5}$,CD是AB边上的高.则BD等于( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | $\frac{2\sqrt{5}}{3}$ |
20.某商品的标价为每件900元,为了吸引顾客,商店在标价8折的基础上再让利30元销售这种商品,此时仍可获利20%,如果设这种商品的进价为x元,则根据题意,可列出方程为( )
| A. | 20%x-30=900×80%-x | B. | 20%x=900×80%-30-x | ||
| C. | 900×20%=900×80%-x-30 | D. | 900×20%=900×80%+30-x |
4.经过点(-2,1)的反比例函数图象应在( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第二、三象限 | D. | 第一、二象限 |
1.下列方程不是一元二次方程的是( )
| A. | ax+1=x2+x | B. | xy=16 | C. | x2+bx+c=0 | D. | m2=3 |
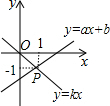 已知函数y=ax+b与函数y=kx的图象相交于点P,根据图象,可得关于x、y的二元一次方程组$\left\{\begin{array}{l}{ax-y+b=0}\\{kx-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$.
已知函数y=ax+b与函数y=kx的图象相交于点P,根据图象,可得关于x、y的二元一次方程组$\left\{\begin{array}{l}{ax-y+b=0}\\{kx-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$. 已知正六边形ABCDEF内接于⊙O,图中阴影部分的面积为27$\sqrt{3}$,则⊙O的半径为6.
已知正六边形ABCDEF内接于⊙O,图中阴影部分的面积为27$\sqrt{3}$,则⊙O的半径为6.