题目内容
13.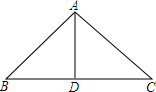 如图,一只蜘蛛在等腰Rt△ABC钢梁上织网纲,∠BAC=90°,AB=AC=8,E在AB上,BE=2,要在顶梁柱AD(中线)上定一点F,从B点到F点拉网纲,再从F点到E点拉网纲.
如图,一只蜘蛛在等腰Rt△ABC钢梁上织网纲,∠BAC=90°,AB=AC=8,E在AB上,BE=2,要在顶梁柱AD(中线)上定一点F,从B点到F点拉网纲,再从F点到E点拉网纲.(1)F点在AD(中线)上何处时网纲(BF+FE)最短,并证明.
(2)在(1)中,求最短网纲(BF+FE)的长度.
(3)在AB上还有点E1、E2,已知BE=EE1=E1E2=E2A=2,现在蜘蛛要在B、E两点之间,E、E1两点之间,E1、E2两点之间都要到顶梁柱AD上定一次点拉网纲,直到E2点结束,求这些网纲之和最短时的长度?
分析 (1)利用轴对称求最短路径得出F点位置,进而利用三角形三边关系得出答案;
(2)利用等腰直角三角形的性质结合勾股定理的出答案;
(3)利用(2)中解题思路,结合勾股定理求出答案.
解答 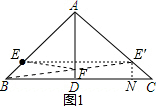 解:(1)如图1:作E点关于直线AD的对称点E′,连接BE′,交AD于点F,
解:(1)如图1:作E点关于直线AD的对称点E′,连接BE′,交AD于点F,
F点即为所求,
证明:由对称的性质可得:EF=FE′,此时BE′在一条直线上,在AD上任取一点与B,E′构成三角形,利用三角形两边之和大于第三边可得BE′最小,即可得出,BF+FE最短;
(2)如图1,过点E′,作E′N⊥BC于点N,
∵∠BAC=90°,AB=AC=8,
∴BC=8$\sqrt{2}$,
∵BE=2,则CE′=2,
∴E′C=NC=$\sqrt{2}$,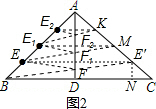 ∴BN=7$\sqrt{2}$,
∴BN=7$\sqrt{2}$,
在△BNE′中,BE′=$\sqrt{(7\sqrt{2})^{2}+(\sqrt{2})^{2}}$=10;
(3)如图2,由(2)可得:BF+EF=10,
同理可得:EF1+E1F1=EM=$\sqrt{52}$=2$\sqrt{13}$,E1K=E1F2+E2F2=$\sqrt{20}$=2$\sqrt{5}$,
故这些网纲之和最短时的长度和为:10+2$\sqrt{13}$+2$\sqrt{5}$.
点评 此题主要考查了利用轴对称取最短路线以及勾股定理,正确利用轴对称求出F点位置是解题关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
8.已知x,y为实数,且$\sqrt{x-1}$+3|y-2|=0,则x-y的值为( )
| A. | 3 | B. | -3 | C. | -1 | D. | 1 |
2.某服装店购进了30套保暖内衣,销售时,针对不同的顾客,这30套保暖内衣的售价不完全相同,若以100元为标准,将超过的钱数记为正,不足的钱数记为负,则记录结果如表所示:
(1)与标准价格相比,30件保暖内衣总售价超过或不足多少元?
(2)若该服装店每件进价为80元,则盈利多少元?
| 售出件数 | 7 | 6 | 7 | 8 | 2 |
| 售价(元) | +5 | +1 | 0 | -2 | -5 |
(2)若该服装店每件进价为80元,则盈利多少元?
 如图,直线AB、CD相交于O,OE平分∠AOC,若∠AOE=23°,则∠BOD=46°.
如图,直线AB、CD相交于O,OE平分∠AOC,若∠AOE=23°,则∠BOD=46°.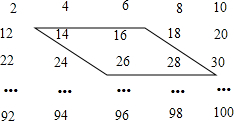 下列数阵是由50个偶数排成的.
下列数阵是由50个偶数排成的. 如图,已知△ABC中,AB=BC,点E是AC边上的中点,过点E作DE∥BC,求证:△BDE是等腰三角形.
如图,已知△ABC中,AB=BC,点E是AC边上的中点,过点E作DE∥BC,求证:△BDE是等腰三角形.