题目内容
3. 如图,已知△ABC中,AB=BC,点E是AC边上的中点,过点E作DE∥BC,求证:△BDE是等腰三角形.
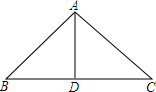
如图,已知△ABC中,AB=BC,点E是AC边上的中点,过点E作DE∥BC,求证:△BDE是等腰三角形.
分析 根据等腰三角形的性质得到∠ABE=∠CBE,根据平行线的性质得到∠DEB=∠CBE,等量代换得到∠DEB=∠ABE,即可得到结论.
解答 证明:∵△ABC中,AB=BC,点E是AC边上的中点,
∴∠ABE=∠CBE,
∵DE∥BC,
∴∠DEB=∠CBE,
∴∠DEB=∠ABE,
∴△BDE是等腰三角形.
点评 本题考查了等腰三角形的判定及性质和平行线的性质;进行角的等量代换是正确解答本题的关键.

练习册系列答案
相关题目
 如图,一只蜘蛛在等腰Rt△ABC钢梁上织网纲,∠BAC=90°,AB=AC=8,E在AB上,BE=2,要在顶梁柱AD(中线)上定一点F,从B点到F点拉网纲,再从F点到E点拉网纲.
如图,一只蜘蛛在等腰Rt△ABC钢梁上织网纲,∠BAC=90°,AB=AC=8,E在AB上,BE=2,要在顶梁柱AD(中线)上定一点F,从B点到F点拉网纲,再从F点到E点拉网纲. 如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数y=$\frac{1}{3}$x2与y=-$\frac{1}{3}$x2的图象,则阴影部分的面积是8.
如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数y=$\frac{1}{3}$x2与y=-$\frac{1}{3}$x2的图象,则阴影部分的面积是8. 如图,AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E.CE=1,ED=3,
如图,AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E.CE=1,ED=3, △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示.