题目内容
如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F.
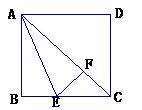
(1)观察图形,写出图中与BE相等的线段.
(2)选择图中与BE相等的任意一条线段,并加以证明.
(1)EF=FC.(2)证明见解析.
【解析】(1)EF和FC;
∵AE平分∠BAC,EF⊥AC交AC于点F,BE⊥AB,∴BE=EF;又∵AC是正方形ABCD的对角线,∴∠ECF=45°,∴∠CEF=45°,∴EF=FC.
(2)∵四边形ABCD是正方形,∴∠B=90°,又∵EF⊥AC,∴∠AFE=∠B,∵AE平分∠BAC,∴∠BAE=∠FAE,在△ABE和△AFE中 ,∴△ABE≌△AFE(AAS),
,∴△ABE≌△AFE(AAS),
∴BE=EF.

练习册系列答案
相关题目
 、
、 、
、 、… ,按如图所示的方式放置.点
、… ,按如图所示的方式放置.点 、
、 、
、 、…和点
、…和点 、
、 、
、 、…分别在直线
、…分别在直线 和
和 轴上,则第2015个正方形
轴上,则第2015个正方形 的边长为_____________.
的边长为_____________.
 与
与 相离,
相离, 于点
于点 ,交
,交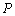 ,点
,点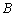 是
是 ,连接
,连接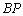 并延长,交直线
并延长,交直线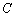 ,使得
,使得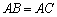 .
.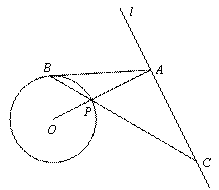
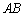 是
是 ,
,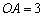 ,求
,求 的长.
的长. 的解是 .
的解是 .
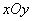 中,直线
中,直线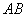 经过点
经过点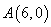 、
、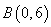 ,⊙
,⊙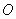 的半径为2(
的半径为2(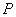 是直线
是直线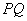 ,
,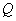 为切点,则切线长
为切点,则切线长
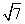 B.
B.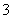 C.
C.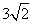 D.
D.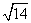
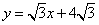 与x轴、y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于C.
与x轴、y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于C.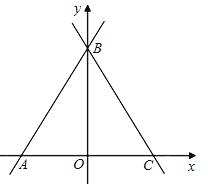
 面内是否存在一点N,使以A、Q、M、N为顶点的四边形为菱形?若存在,请直接写出N点的坐标;若不存在,请说明理由.
面内是否存在一点N,使以A、Q、M、N为顶点的四边形为菱形?若存在,请直接写出N点的坐标;若不存在,请说明理由. 、
、 b为非负实数,则当代数式
b为非负实数,则当代数式
 取得最小值时,
取得最小值时, = 。
= 。