题目内容
12.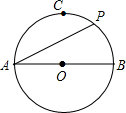 如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$的中点,则∠PAB的度数( )
如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$的中点,则∠PAB的度数( )| A. | 30° | B. | 25° | C. | 22.5° | D. | 不能确定 |
分析 连接OC、OP,根据AB是直径、点C是$\widehat{AB}$的中点、点P是$\widehat{BC}$的中点,即可得出∠POB的度数,再结合圆周角定理即可得出结论.
解答 解:连接OC、OP,如图所示.
∵AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$的中点,
∴∠POB=$\frac{1}{2}$×$\frac{1}{2}$×180°=45°,
∴∠PAB=$\frac{1}{2}$∠POB=22.5°.
故选C.
点评 本题考查了圆周角定理以及圆心角、弧、弦的关系,根据弦与弧的关系找出∠POB=45°是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.已知a>0,b<0,且|b|>|a|,则a,-a,b,-b按从小到大的顺序排列( )
| A. | -b<a<-a<b | B. | b<-a<a<-b | C. | a<-a<-b<b | D. | -a<a<b<-b |
3.在下列各数中:0,3.1415926,$\frac{22}{7}$,π,15%,-2.363636…,正分数的个数是( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
4.计算(2×104)4等于( )
| A. | 16×1016 | B. | 1.6×1017 | C. | 2×1016 | D. | 8×108 |
2.把方程x2-6x+2=0配方成(x+p)2=q的形式后,p与q的值分别是( )
| A. | 3,7 | B. | -3,7 | C. | 9,7 | D. | -3,9 |
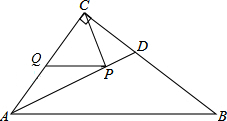 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=8,AD是∠BAC的平分线,若点P,Q分别是AD和AC上的动点,则PC+PQ的最小值是4.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=8,AD是∠BAC的平分线,若点P,Q分别是AD和AC上的动点,则PC+PQ的最小值是4.