题目内容
1.从-1、0、1、2这四个数中,任取一个数记为b,再从余下的三个数中任取一个记为c,则二次函数y=x2-bx+c的图象与x轴有两个交点的概率为$\frac{1}{2}$.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所取的数能使二次函数的图象与x轴有两个交点的情况,再利用概率公式即可求得答案.
解答 解:画树状图如下:
由树状图可知,共有12种等可能结果,其中能使二次函数y=x2-bx+c的图象与x轴有两个交点的有6种结果,
∴二次函数y=x2-bx+c的图象与x轴有两个交点的概率为$\frac{6}{12}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查的是用列表法或画树状图法求概率以及二次函数的性质.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
12.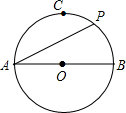 如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$的中点,则∠PAB的度数( )
如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$的中点,则∠PAB的度数( )
 如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$的中点,则∠PAB的度数( )
如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$的中点,则∠PAB的度数( )| A. | 30° | B. | 25° | C. | 22.5° | D. | 不能确定 |
9.下列几何体中截面不是三角形的是( )
| A. | 圆柱 | B. | 圆锥 | C. | 正方体 | D. | 正六棱柱 |
16.在等腰三角形ABC中,∠A=60°,BC=4,则△ABC的周长为( )
| A. | 12 | B. | 14 | C. | 10 | D. | 16 |
6.刚刚离我们而去的台风“杜鹃”虽然没有正面袭击浙江,但还是给浙江省造成的直接经济损失达16.9亿元,近似数16.9亿精确到( )
| A. | 十分位 | B. | 千万位 | C. | 亿位 | D. | 十亿位 |
11.下列说法正确的是( )
| A. | 三角形三条高的交点都在三角形内 | |
| B. | 三角形的角平分线是射线 | |
| C. | 三角形三边的垂直平分线不一定交于一点 | |
| D. | 三角形三条中线的交点在三角形内 |