题目内容
2.把方程x2-6x+2=0配方成(x+p)2=q的形式后,p与q的值分别是( )| A. | 3,7 | B. | -3,7 | C. | 9,7 | D. | -3,9 |
分析 直接对一元二次方程配方,然后把常数项移到等号右边即可.
解答 解:x2-6x=-2,
x2-6x+9=-2+9,
(x-3)2=7,
∴p=-3,q=7
故选:B.
点评 本题考查了配方法解一元二次方程,用配方法解一元二次方程的步骤:
①把原方程化为ax2+bx+c=0(a≠0)的形式;②方程两边同除以二次项系数,使二次项系数为1,并把常数项移到方程右边;③方程两边同时加上一次项系数一半的平方;④把左边配成一个完全平方式,右边化为一个常数;⑤如果右边是非负数,就可以进一步通过直接开平方法来求出它的解,如果右边是一个负数,则判定此方程无实数解.

练习册系列答案
相关题目
12.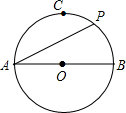 如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$的中点,则∠PAB的度数( )
如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$的中点,则∠PAB的度数( )
 如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$的中点,则∠PAB的度数( )
如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$的中点,则∠PAB的度数( )| A. | 30° | B. | 25° | C. | 22.5° | D. | 不能确定 |
14.下面四个实数中,是无理数的是( )
| A. | 0 | B. | -$\sqrt{2}$ | C. | 3.1415 | D. | $\frac{3}{7}$ |
11.下列说法正确的是( )
| A. | 三角形三条高的交点都在三角形内 | |
| B. | 三角形的角平分线是射线 | |
| C. | 三角形三边的垂直平分线不一定交于一点 | |
| D. | 三角形三条中线的交点在三角形内 |
12.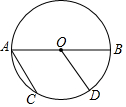 如图,已知AB是⊙O的直径,$\widehat{CD}$=$\widehat{BD}$,则下列结论中正确的是( )
如图,已知AB是⊙O的直径,$\widehat{CD}$=$\widehat{BD}$,则下列结论中正确的是( )
 如图,已知AB是⊙O的直径,$\widehat{CD}$=$\widehat{BD}$,则下列结论中正确的是( )
如图,已知AB是⊙O的直径,$\widehat{CD}$=$\widehat{BD}$,则下列结论中正确的是( )| A. | AC=OD | B. | AC∥OD | C. | $\widehat{AC}$=$\widehat{CD}$ | D. | $\widehat{AC}$=$\widehat{BD}$ |