题目内容
如图，?ABCD中，点E，F在AD上，且BE平分∠ABC，CF平分∠BCD．求证：AF=ED．
考点：平行四边形的性质
专题：证明题
分析：利用平行四边形的性质得出∠AEB=∠EBC，进而得出AB=AE，同理得出DC=DF，进而得出AF=ED．
解答：证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AB=DC．
∴∠AEB=∠EBC．
∵BE平分∠ABC，
∴∠ABE=∠EBC．
∴∠AEB=∠ABE．
∴AB=AE．
同理DC=DF．
∴AE=DF．
∴AE-FE=DF-FE，即AF=ED．
∴AD∥BC，AB=DC．
∴∠AEB=∠EBC．
∵BE平分∠ABC，
∴∠ABE=∠EBC．
∴∠AEB=∠ABE．
∴AB=AE．
同理DC=DF．
∴AE=DF．
∴AE-FE=DF-FE，即AF=ED．
点评：此题主要考查了平行四边形的性质，得出AB=AE是解题关键．
练习册系列答案
相关题目
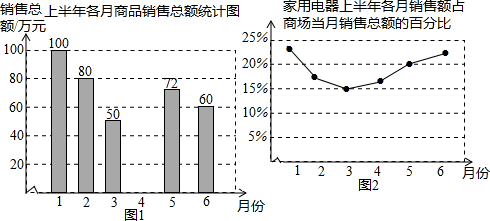
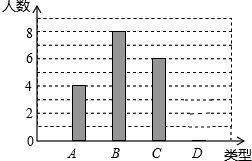某校240名学生参加植树活动，要求每人植树4～7棵，活动结束后抽查了20名学生每人的植树量，并分为四类：A类4棵、B类5棵、C类6棵、D类7棵，将各类的人数绘制成如图所示不完整的条形统计图，回答下列问题：
为了了解八年级800名学生寒假的读书情况，数学小组随机调查了50名八年级学生，并将统计数据制成了扇形统计图如图，其中读1册的有13人，则该校八年级学生中读书册数为3册的约有
如图，在等腰梯形ABCD中，AD∥BC，DE⊥BC，BD⊥DC，垂足分别为E，D，DE=3，BD=5，则等腰梯形ABCD的周长等于