Question

【题目】在平面直角坐标系中，已知第一象限内的点在反比例函数y＝的图象上，第二象限内的点B在反比例函数y＝的图象上，连接、，若，，则__________．

Answer 1

【答案】

【解析】

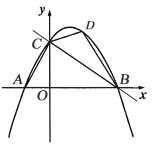
过点A作AE⊥x轴于点E，过点B作BF⊥x轴于点F，设点A的坐标为（a，），点B的坐标为（b，），判断出△OBF∽△AOE，利用对应边成比例可求出k的值．

过点A作AE⊥x轴于点E，过点B作BF⊥x轴于点F，
设点A的坐标为（a，），点B的坐标为（b，），
∵∠AOE+∠BOF=90°，∠OBF+∠BOF=90°，
∴∠AOE=∠OBF，
又∵∠BFO=∠OEA=90°，
∴△OBF∽△AOE，
∴ ，即 ，
则 b①，a= ②，
①×②可得：-2k=1，
解得：k=．
故答案为：．