题目内容
【题目】某蔬菜专业户试种植了一种紧俏蔬菜（都能卖出），其中每千克的成本
在9元/千克的基础上，还有一些上浮．若浮动价（元/
）与需求量
（千克）成反比，比例系数为30．市场连续四天调查发现，蔬菜售价
（元/）与市场需求量
有如下关系：
需求量 | 50 | 40 | 30 | 20 |
蔬菜售价 | 10 | 15 | 20 | 25 |
（1）直接写出每千克的成本与需求量的关系式_________；
（2）求与的关系式；
（3）当某天的利润率达到
时，求这天的需求量；
（4）求需求量是多少千克时，利润达到最大值，最大值是多少？
【答案】（1）
；（2）
；（3）30千克或4千克；（4）当26千克时取得最大利润是308元
【解析】
（1）先根据题意表示出浮动价（元/
）与需求量
（千克）的反比例函数关系再加上成本价9元即可.
（2）观察图表可发现蔬菜售价
（元/）与市场需求量
为一次函数关系，设其解析式
，代入两点解答即可.
（3）利润率达到
，其关系表示即为
，将两函数表达式代入转化为关于的方程解答即可.
（4）将利润表示为关于市场需求量的二次函数关系式，用配方法求最值即可.
解：（1）
（2）观察发现需求量每减少10千克，蔬菜售价会增加5元/，是一次函数关系
设，把
和
代入得
解得：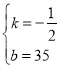
则
（3）法1：每天的利润
每天的总成本：
当
时，
整理得：
，
法2：∵利润率
∴
整理得，
∴，
经检验，是原方程的解
（4）
因为
所以函数有最大值，当
时取得最大利润，为308元．
阅读快车系列答案
【题目】在推进郑州市城乡生活垃圾分类的行动中，某社区对居民掌握垃圾分类知识的情况进行调査．其中
，
两小区分别有1000名居民参加了测试，社区从中各随机抽取50名居民成绩进行整理得到部分信息：
（信息一）小区50名居民成绩的频数直方图如下(每一组含前一个边界值，不含后一个边界值)．
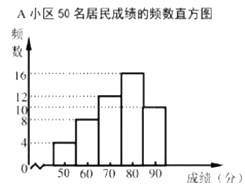
（信息二）上图中，从左往右第四组的成绩如下：
75 | 75 | 79 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
（信息三），两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺)：
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
| 75.1 | 79 | 40% | 277 | |
| 75.1 | 77 | 76 | 45% | 211 |
根据以上信息，回答下列问题：
（1）求小区50名居民成绩的中位数．
（2）请估计小区1000名居民成绩能超过平均数的人数．
（3）请尽量从多个角度(至少三个)，选择合适的统计量分析，两小区参加测试的居民掌握垃圾分类知识的情况．
