Question

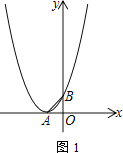
【题目】已知抛物线顶点A在x轴负半轴上，与y轴交于点B，OB＝1，△OAB为等腰直角三角形

（1）求抛物线的解析式

（2）若点C在抛物线上，若△ABC为直角三角形，求点C的坐标

（3）已知直线DE过点（－1，－4），交抛物线于点D、E，过D作DF∥x轴，交抛物线于点F，求证：直线EF经过一个定点，并求定点的坐标

Answer 1

【答案】（1）；（2）；（3）见解析，定点

【解析】

（1）根据题意可得出点A的坐标，用顶点式求解抛物线解析式即可；

（2）设点C的坐标为(x,y)，利用勾股定理的逆定理分三种情况讨论即可；

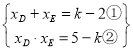（3）设的解析式为，联立直线DE与抛物线解析式得出，从而得出，继而得出，再设的解析式为，通过联立得出，进一步得出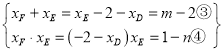，联立①②③④得，所以，过定点

解：（1）根据题意可得出抛物线顶点的坐标为(-1,0)，

∴抛物线的解析式为：；

（2）设点C的坐标为(x,y)，，A(-1,0)，B(0,1)，

当为直角顶点时，，

∴，

整理得：，

∵，

∴，

解得：（舍去），

∴，

∴点C的坐标为；

同理，当为直角顶点时，，

∴，

整理得：，

∵，

∴，

解得：（舍去），

∴，

∴点C的坐标为；

当为直角顶点时，不存在符合条件的点C；

（3）设的解析式为，联立，

得，，

∴，

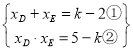∵、F关于对称轴对称，

∴，

设的解析式为，

联立，

得，，

∴，

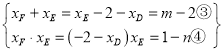联立①②③④得，

∴，过定点．