题目内容
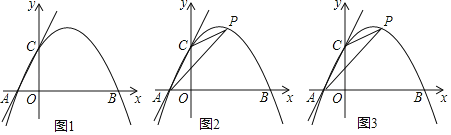
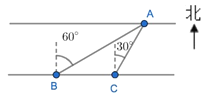
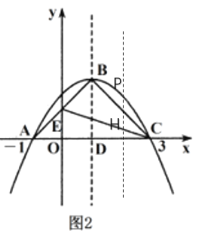
【题目】如图，抛物线y＝ax2＋bx＋c与x轴交于点A（－1，O）、C（3，0），点B为抛物线顶点，直线BD为抛物线的对称轴，点D在x轴上，连接AB、BC.
⑴如图1，若∠ABC＝60°，则点B的坐标为______________；
⑵如图2，若∠ABC＝90°，AB与y轴交于点E，连接CE.
①求这条抛物线的解析式；
②点P为第一象限抛物线上一个动点，设△PEC的面积为S，点P的横坐标为m，求S关于m的函数关系武，并求出S的最大值；
③如图3，连接OB，抛物线上是否存在点Q，使直线QC与直线BC所夹锐角等于∠OBD，若存在请直接写出点Q的坐标；若不存在，说明理由.
【答案】（1）
；（2）①
；②
，S的最大值
；③
或
.
【解析】
（1）∠ABC=60°，故△ABC为等边三角形，即可求解；
⑵①点B的坐标为（1，2），抛物线的表达式为：y=a（x-1）2+2，将点A的坐标代入上式，即可求解；
②分别求出直线AB、CE的表达式，过点P作PH∥y轴交EC于点H，用含m的式子表示出PH和OC,根据
列出函数关系式并求出最值即可；
③在BD上作点F,使DF=BD，连接CF.过点F作FG∥x轴，分别交CQ于点M、交BC的延长线于点G，过点M作MH⊥CE于点H，则△CFG为等腰直角三角形，设HG=MH=n，求出
，得到点M坐标为
，进一步求出直线CM的表达式为：y=-3x+9；再将直线CM解析式与抛物线解析式联立成方程组，求解得点Q的坐标.
解：（1）∠ABC=60°，故△ABC为等边三角形，
AC=4，则
函数对称轴为x=1，故点B
故答案是；
（2）①AC=4，则点B的坐标为（1，2），
抛物线的表达式为：y=a（x-1）2+2，
将点A的坐标代入上式得：0=a（-2）2+2，解得：
函数的表达式为：
；
②将点A、B坐标代入一次函数表达式：y=kx+b得：
解得：
直线AB的表达式为：y=x+1，则点E（0，1），
同理可得直线CE的表达式为：
过点P作PH∥y轴交EC于点H，
则点
，点
则
∴S有最大值，当
时，最大值为：
③存在，点Q的坐标为或.
理由：
如图3，在BD上作点F,使DF=BD，连接CF.过点F作FG∥x轴，分别交CQ于点M、交BC的延长线于点G，过点M作MH⊥CE于点H，则△CFG为等腰直角三角形，
∵AC=4，则
，QC与直线BC所夹锐角等于∠OBD，即：
设：HG=MH=n，则CH=2n，即
则点M坐标为
可解得直线CM的表达式为：y=-3x+9
将直线CM解析式与抛物线解析式联立成方程组，并解得
或
即点Q的坐标为或
