题目内容
3.某校机器人兴趣小组在如图①所示的矩形场地上开展训练.机器人从点A出发,在矩形ABCD边上沿着A→B→C→D的方向匀速移动,到达点D时停止移动.已知机器人的速度为1个单位长度/s,移动至拐角处调整方向需要1s(即在B、C处拐弯时分别用时1s).设机器人所用时间为t(s)时,其所在位置用点P表示,P到对角线BD的距离(即垂线段 PQ的长)为d个单位长度,其中d与t的函数图象如图②所示.(1)求AB、BC的长;
(2)如图②,点M、N分别在线段EF、GH上,线段MN平行于横轴,M、N的横坐标分别为t1、t2.设机器人用了t1(s)到达点P1处,用了t2(s)到达点P2处(见图①).若CP1+CP2=7,求t1、t2的值.
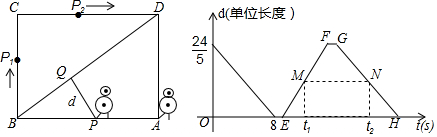
分析 (1)作AT⊥BD,垂足为T,由题意得到AB=8,AT=$\frac{24}{5}$,在Rt△ABT中,根据勾股定理得到BT=$\frac{32}{5}$,根据三角函数的定义即可得到结论;
(2)如图,连接P1P2.过P1,P2分别作BD的垂线,垂足为Q1,Q2.则P1Q1∥P2Q2.根据平行线的性质得到d1=d2,得到P1Q1=P2Q2.根据平行线分线段成比例定理得到$\frac{{C{P_1}}}{6}=\frac{{C{P_2}}}{8}$.设M,N的横坐标分别为t1,t2,于是得到结论.
解答  解:(1)作AT⊥BD,垂足为T,由题意得,AB=8,AT=$\frac{24}{5}$,
解:(1)作AT⊥BD,垂足为T,由题意得,AB=8,AT=$\frac{24}{5}$,
在Rt△ABT中,AB2=BT2+AT2,
∴BT=$\frac{32}{5}$,
∵tan∠ABD=$\frac{AD}{AB}=\frac{AT}{BT}$,
∴AD=6,
即BC=6;
(2)在图①中,连接P1P2.过P1,P2分别作BD的垂线,垂足为Q1,Q2.
则P1Q1∥P2Q2.
∵在图②中,线段MN平行于横轴,
∴d1=d2,即P1Q1=P2Q2.∴
P1P2∥BD.
∴$\frac{{C{P_1}}}{CB}=\frac{{C{P_2}}}{CD}$.
即$\frac{{C{P_1}}}{6}=\frac{{C{P_2}}}{8}$.
又∵CP1+CP2=7,
∴CP1=3,CP2=4.
设M,N的横坐标分别为t1,t2,
由题意得,CP1=15-t1,CP2=t2-16,
∴t1=12,t2=20.
点评 本题考查了动点问题的函数图象,勾股定理矩形的性质,平行线分线段成比例定理,正确的作出辅助线是解题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
13.一元一次不等式组$\left\{\begin{array}{l}2x>x-1\\ \frac{1}{2}x≤1\end{array}\right.$的解集是( )
| A. | x>-1 | B. | x≤2 | C. | -1<x≤2 | D. | x>-1或x≤2 |
13.已知$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$,都是方程y=kx+b的解,则k和b的值是( )
| A. | $\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{k=0}\\{b=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{k=2}\\{b=-3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{k=1}\\{b=-2}\end{array}\right.$ |
14.完成下列任务,适合用抽样调查的是( )
| A. | 为订购校服,了解学生衣服的尺寸 | |
| B. | 对航天飞机上的零部件进行检查 | |
| C. | 考察一批炮弹的杀伤半径 | |
| D. | 语文老师检查某学生一篇作文中的错别字 |
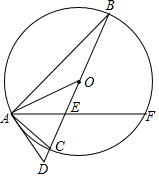 如图,△ABC内接于⊙O,BC是⊙O的直径,弦AF交BC于点E,延长BC到点D,连接OA,AD,使得∠FAC=∠AOD,∠D=∠BAF.
如图,△ABC内接于⊙O,BC是⊙O的直径,弦AF交BC于点E,延长BC到点D,连接OA,AD,使得∠FAC=∠AOD,∠D=∠BAF.