Question

1．已知：△ABC中，AB=5，AC=4，BC边上的高AD=3，则边BC的长为4+$\sqrt{7}$或4-$\sqrt{7}$．

Answer 1

分析 分两种情况考虑：如图1所示，此时△ABC为锐角三角形，在直角三角形ABD与直角三角形ACD中，利用勾股定理求出BD与DC的长，由BD+DC求出BC的长即可；如图2所示，此时△ABC为钝角三角形，同理由BD-CD求出BC的长即可．

解答 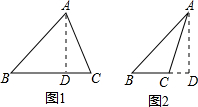解：分两种情况考虑：
如图1所示，此时△ABC为锐角三角形，
在Rt△ABD中，根据勾股定理得：BD=$\sqrt{{AB}^{2}-{AD}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4；
在Rt△ACD中，根据勾股定理得：CD=$\sqrt{{AC}^{2}-{AD}^{2}}$=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$，
此时BC=BD+DC=4+$\sqrt{7}$；
如图2所示，此时△ABC为钝角三角形，
在Rt△ABD中，根据勾股定理得：BD=$\sqrt{{AB}^{2}-{AD}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4；
在Rt△ACD中，根据勾股定理得：CD=$\sqrt{{AC}^{2}-{AD}^{2}}$=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$，
此时BC=BD-DC=4-$\sqrt{7}$，
综上，BC的长为4+$\sqrt{7}$或4-$\sqrt{7}$．
故答案为：4+$\sqrt{7}$或4-$\sqrt{7}$．

点评 本题考查的是勾股定理，在解答此题时要注意进行分类讨论，不要漏解．