题目内容
6.分解因式:x2-$\frac{1}{4}$y2=(x+$\frac{1}{2}$y)(x-$\frac{1}{2}$y).ab-a-b+1=(b-1)(a-1).分析 根据平方差公式分解即可;先分组,再分解因式,最后提取公因式即可.
解答 解:x2-$\frac{1}{4}$y2=(x+$\frac{1}{2}$y)(x-$\frac{1}{2}$y),
ab-a-b+1
=(ab-a)-(b-1)
=a(b-1)-(b-1)
=(b-1)(a-1),
故答案为:(x+$\frac{1}{2}$y)(x-$\frac{1}{2}$y),(b-1)(a-1).
点评 本题考查了分解因式的应用,能选择适当的方法分解因式是解此题的关键.

练习册系列答案
相关题目
14.判断点(2,4)不在下列哪个函数的图象上?( )
| A. | y=2x | B. | y=2x+4 | C. | y=$\frac{8}{x}$ | D. | y=$\frac{1}{2}$x+3 |
11.在有理数中有( )
| A. | 最大的数 | B. | 最小的数 | C. | 绝对值最小的数 | D. | 不能确定 |
18.下列各数中,比-3小的数是( )
| A. | -$\frac{1}{3}$ | B. | 0 | C. | -2 | D. | -4 |
16.一个多边形的内角和等于1260°,则从此多边形一个顶点引出的对角线有( )
| A. | 4条 | B. | 5条 | C. | 6条 | D. | 7条 |
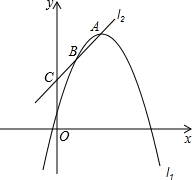 如图,已知,抛物线l1:y=ax2-4ax+5+4a(a<0)的顶点为A,直线l2:y=kx+3过点A,直线l2与抛物线l1及y轴分别交于B,C.
如图,已知,抛物线l1:y=ax2-4ax+5+4a(a<0)的顶点为A,直线l2:y=kx+3过点A,直线l2与抛物线l1及y轴分别交于B,C.