题目内容
已知,如图,双曲线y=
 (x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线y=
(x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线y=
 (x>0)交于点C,点D,则:
(x>0)交于点C,点D,则:
(1)AB与CD的位置关系是 ;
(2)四边形ABDC的面积为 .


【考点】反比例函数与一次函数的交点问题.
【分析】(1)首先过点A作AM⊥x轴于点M,过点D作DH⊥x轴于点H,过点B作BN⊥x轴于点N,由双曲线y=
 (x>0)与直线EF交于点A、点B,且AE=AB=BF,可设点A的坐标为(m,
(x>0)与直线EF交于点A、点B,且AE=AB=BF,可设点A的坐标为(m,
 ),得到点B的坐标为:(2m,
),得到点B的坐标为:(2m,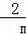
 ),则可由S△OAB=S△OAM+S梯形AMNB﹣S△OBN,求得△AOB的面积,易得△ODH∽△OBN,可得(
),则可由S△OAB=S△OAM+S梯形AMNB﹣S△OBN,求得△AOB的面积,易得△ODH∽△OBN,可得(
 )2=
)2=
 =
=
 ,继而可得
,继而可得
 =
=
 ,所以AB∥CD
,所以AB∥CD
(2)由
 =
=
 ,∠COD=∠AOB则可证得△COD∽△AOB,然后由相似三角形面积比等于相似比的平方,求得答案.
,∠COD=∠AOB则可证得△COD∽△AOB,然后由相似三角形面积比等于相似比的平方,求得答案.
【解答】解:(1)如图,过点A作AM⊥x轴于点M,过点D作DH⊥x轴于点H,过点B作BN⊥x轴于点N,
∴AM∥DH∥BN∥y轴,
设点A的坐标为:(m,
 ),
),
∵AE=AB=BF,
∴OM=MN=NF,
∴点B的坐标为:(2m,
 ),
),
∴S△OAB=S△OAM+S梯形AMNB﹣S△OBN=2+
 ×(
×(
 +
+
 )×(2m﹣m)﹣2=3,
)×(2m﹣m)﹣2=3,
∵DH∥BN,
∴△ODH∽△OBN,
∴
 =
=
 =
=
 ,
,
∵DH•OH=2,BN•ON=4,
∴(
 )2=
)2=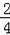
 =
=
 ,
,
同理:(
 )2=
)2=
 ,
,
∴
 =
=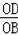
 ,
,
∴AB∥CD
故答案为:AB∥CD
(2)∵
 =
=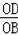
 ,∠COD=∠AOB,
,∠COD=∠AOB,
∴△COD∽△AOB,
∴
 =(
=(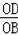
 )2=
)2=
 ,
,
∴S△COD=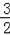
 ,
,
∴S四边形ABDC=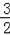
 .
.
故答案为: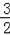
 .
.


【点评】此题考查了反比例函数中k的几何意义以及相似三角形的判定与性质.此题难度较大,注意掌握辅助线的作法,注意掌握方程思想与数形结合思想的应用.

 阅读快车系列答案
阅读快车系列答案某大型超市上周日购进新鲜的黄瓜1000公斤,每公斤1.5元,受暴发的“毒黄瓜”的影响,销售价格出现较大的波动,表中为一周内黄瓜销售价格的涨跌情况(涨为正,跌为负,其中星期一的销售价格是与进价比较,单位:元):
| 星 | 一 | 二 | 三 | 四 | 五 | 六 |
| 每公斤销售价涨跌(与前一天比较) | +0.3 | +0.4 | ﹣0.5 | ﹣0.6 | ﹣0.7 | +0.1 |
(1)到星期二时,每公斤的黄瓜售价是多少元?
(2)本周最低售价是每公斤多少元?
(3)已知截止到星期五,已卖出黄瓜700公斤,销售总额为935元.如果超市星期六能将剩下的黄瓜全部卖出.不考虑损耗等其他因素,请算算该超市本周销售黄瓜是盈还是亏?盈亏是多少?



 B、
B、 C、
C、 D、
D、

 ÷
÷
 ,然后选取一个合适的a值,代入求值.
,然后选取一个合适的a值,代入求值. 的相反数是( )
的相反数是( ) B.
B. C.
C.
 期
期 ,则m
,则m 的取值范围是__________。
的取值范围是__________。