题目内容
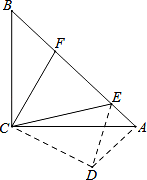
已知,如图,在 Rt△ABC 中,∠ACB=90°,AC=BC,点 E、F 分别是斜边 AB 上的两点,且∠FCE=45°.
(1)现将 CF 绕点 C 顺时针旋转 90°到 CD,连结 AD.求证:AD=BF. 若 EF=10,BF=8.求 AE 的长及△ABC 的面积.
【考点】旋转的性质;全等三角形的判定与性质;勾股定理.
【分析】(1)证明△BCF≌△ACD,根据全等三角形的对应边相等即可证得; 首先证明△ECF≌△ECD,则 ED=EF,然后在直角△ADE 中利用勾股定理求得 AE 的长,则 AB 的 长即可求得,然后利用三角函数求得 AC 和 BC 的长,利用三角形的面积公式求解.
 【解答】(1)证明:在△BCF 和△ACD 中,
【解答】(1)证明:在△BCF 和△ACD 中,
,
∴△BCF≌△ACD,
∴AD=BF,∠CAD=∠CBA=45°.
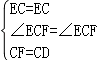 解:∵在△ECF 和△ECD 中,
解:∵在△ECF 和△ECD 中,
,
∴△ECF≌△ECD,
∴ED=EF,
 则在 Rt△DAE 中,由勾股定理可得:AE= =6,
则在 Rt△DAE 中,由勾股定理可得:AE= =6,

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
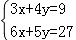 ,则 8x+8y=
,则 8x+8y= 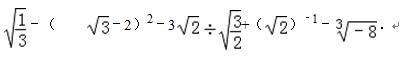
 A. 直线AB与直线BA是同一条直线
A. 直线AB与直线BA是同一条直线