题目内容
甲组的 4 名工人 3 月份完成的总工作量比此月人均定额的 4 倍多 20 件,乙组的 5 名工人 3 月份
完成的总工作量比此月人均定额的 6 倍少 20 件.
(1)如果两组工人实际完成的此月人均工作量相等,那么此月人均定额是多少件? 如果甲组工人实际完成的此月人均工作量比乙组的多 2 件,则此月人均定额是多少件?
(3)如果甲组工人实际完成的此月人均工作量比乙组的少 2 件,则此月人均定额是多少件?
【考点】一元一次方程的应用.
【专题】工程问题.
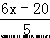 【分析】设此月人均定额为 x 件.由题意知:甲组的 4 名工人 3 月份完成的总工作量比此月人均定 额的 4 倍多 20 件,则甲组的总工作量为(4x+20)件,人均为
【分析】设此月人均定额为 x 件.由题意知:甲组的 4 名工人 3 月份完成的总工作量比此月人均定 额的 4 倍多 20 件,则甲组的总工作量为(4x+20)件,人均为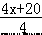 件;乙组的 5 名工人 3 月份完
件;乙组的 5 名工人 3 月份完
成的总工作量比此月人均定额的 6 倍少 20 件,乙组的总工作量为(6x﹣20)件,乙组人均为
件.
(1)可根据甲组人均工作量=乙组人均工作量为等量关系列出方程求解; 可根据甲组人均工作量﹣2=乙组人均工作量为等量关系列出方程求解;
(3)可根据甲组人均工作量=乙组人均工作量﹣2 列出方程求解.
【解答】解:设此月人均定额为 x 件,则甲组的总工作量为(4x+20)件,人均为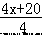 件;乙组的 5 名工人 3 月份完成的总工作量比此月人均定额的 6 倍少 20 件,乙组的总工作量为(6x﹣20)件, 乙组人均为
件;乙组的 5 名工人 3 月份完成的总工作量比此月人均定额的 6 倍少 20 件,乙组的总工作量为(6x﹣20)件, 乙组人均为 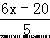 件.
件.
(1)∵两组人均工作量相等,
∴ 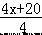 =
= 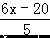 , 解得:x=45. 所以,此月人均定额是 45 件;
, 解得:x=45. 所以,此月人均定额是 45 件;
∵甲组的人均工作量比乙组多 2 件,
∴  ,
,
解得:x=35, 所以,此月人均定额是 35 件;
(3)∵甲组的人均工作量比乙组少 2 件,
∴ 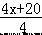 =
= 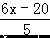 ﹣2, 解得:x=55,
﹣2, 解得:x=55,
所以,此月人均定额是 55 件.
【点评】本题主要考查一元一次方程的应用,关键在于理解清楚题意找出等量关系,列出方程求解.