题目内容
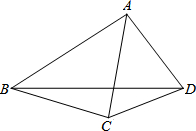如图，在四边形ABCD中，对角线AC平分∠BAD，AB＞AC，下列结论正确的是（ ）| A、AB-AD＞CB-CD |
| B、AB-AD=CB-CD |
| C、AB-AD＜CB-CD |
| D、AB-AD与CB-CD的大小关系不确定 |
考点：角平分线的性质
专题：
分析：取AE=AD，然后利用“边角边”证明△ACD和△ACE全等，根据全等三角形对应边相等可得CD=CE，然后利用三角形的任意两边之和大于第三边解答．
解答：
解：如图，取AE=AD，
∵对角线AC平分∠BAD，
∴∠BAC=∠DAC，
在△ACD和△ACE中，
，
∴△ACD≌△ACE（SAS），
∴CD=CE，
∵BE＞CB-CE，
∴AB-AD＞CB-CD．
故选A．
解：如图，取AE=AD，∵对角线AC平分∠BAD，
∴∠BAC=∠DAC，
在△ACD和△ACE中，
|
∴△ACD≌△ACE（SAS），
∴CD=CE，
∵BE＞CB-CE，
∴AB-AD＞CB-CD．
故选A．
点评：本题考查了角平分线的性质，全等三角形的判定与性质，三角形的任意两边之和大于第三边，熟记性质并作辅助线构造出全等三角形是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
根据图中所示的程序计算：若输入的x为-要得到抛物线y=2（x-4）2-1，可以将抛物线y=2x2（ ）
| A、向右平移4个单位长度，再向下平移1个单位长度 |
| B、向右平移4个单位长度，再向上平移1个单位长度 |
| C、向左平移4个单位长度，再向下平移1个单位长度 |
| D、向左平移4个单位长度，再向上平移1个单位长度 |