题目内容
8.已知k为任意实数,随着k的变化,抛物线y=x2-2(k-1)x+k2-3的顶点随之运动,则顶点运动时经过的路径与两条坐标轴围成图形的面积是( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
分析 利用配方法求出顶点坐标,推出顶点在直线y=2x-2上运动,由此即可解决问题.
解答 解:∵y=x2-2(k-1)x+k2-3
=(x-k+1)2+k2-3-(k-1)2
=(x-k+1)2+2k-4,
∴顶点的坐标为(k-1,2k-4)即[(k-1),2(k-1)-2],
∴顶点在直线y=2x-2上运动,
易知直线y=2x-2交x轴于A(1,0),交y轴于B(0,-2),
∴S△AOB=$\frac{1}{2}$×2×1=1,
∴顶点运动时经过的路径与两条坐标轴围成图形的面积是1,
故选A.
点评 本题考查轨迹、二次函数的性质、配方法等知识,解题的关键是灵活运用所学知识解决问题,属于中考选择题中的压轴题.

练习册系列答案
相关题目
18.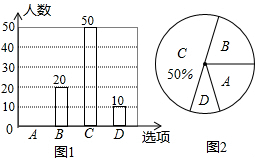 共享单车近日成为市民新宠,越来越多的居民选择共享单车作为出行的交通工具,某中学课外兴趣小组为了了解某小区居民每周使用共享单车时间的情况,随机抽取了该小区部分使用共享单车的居民进行调查(问卷调查表如图所示),并用调查结果绘制了图1、图2两幅每周使用共享单车时间的人数统计图(均不完整),请根据统计图解答以下问题:
共享单车近日成为市民新宠,越来越多的居民选择共享单车作为出行的交通工具,某中学课外兴趣小组为了了解某小区居民每周使用共享单车时间的情况,随机抽取了该小区部分使用共享单车的居民进行调查(问卷调查表如图所示),并用调查结果绘制了图1、图2两幅每周使用共享单车时间的人数统计图(均不完整),请根据统计图解答以下问题:
每周使用共享单车的时间问卷调查表
您好!这是一份关于您平均每周使用共享单车时间的问卷调查表,请在表格中选择一项符合您使用时间的选项,在其后空格内打“√”,非常感谢您的合作.
(1)本次接受问卷调查的共有100人;在扇形统计图中“D”选项所占的百分比为10%;
(2)扇形统计图中,“B”选项所对应扇形圆心角为72度;
(3)请补全条形统计图;
(4)若该小区共有1000名居民,请你估计该小区使用共享单车的时间在“A”选项的有多少人?
 共享单车近日成为市民新宠,越来越多的居民选择共享单车作为出行的交通工具,某中学课外兴趣小组为了了解某小区居民每周使用共享单车时间的情况,随机抽取了该小区部分使用共享单车的居民进行调查(问卷调查表如图所示),并用调查结果绘制了图1、图2两幅每周使用共享单车时间的人数统计图(均不完整),请根据统计图解答以下问题:
共享单车近日成为市民新宠,越来越多的居民选择共享单车作为出行的交通工具,某中学课外兴趣小组为了了解某小区居民每周使用共享单车时间的情况,随机抽取了该小区部分使用共享单车的居民进行调查(问卷调查表如图所示),并用调查结果绘制了图1、图2两幅每周使用共享单车时间的人数统计图(均不完整),请根据统计图解答以下问题:每周使用共享单车的时间问卷调查表
您好!这是一份关于您平均每周使用共享单车时间的问卷调查表,请在表格中选择一项符合您使用时间的选项,在其后空格内打“√”,非常感谢您的合作.
| 选项 | 使用时间t(小时) | |
| A | 0<t≤2 | |
| B | 2<t≤2.5 | |
| C | 2.5<t≤3 | |
| D | t>3 |
(2)扇形统计图中,“B”选项所对应扇形圆心角为72度;
(3)请补全条形统计图;
(4)若该小区共有1000名居民,请你估计该小区使用共享单车的时间在“A”选项的有多少人?
19.下列计算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | 32=6 | C. | (-1)2015=-2015 | D. | |-3|=3 |
20.点A(x,y)的坐标满足xy=0,点A在( )
| A. | x轴上 | B. | y轴上 | C. | 坐标轴上 | D. | 无法确定 |
18.下列语句中,正确的是( )
| A. | 一条直线有且只有一条垂线 | |
| B. | 过一点有且只有一条直线与已知直线平行 | |
| C. | 不相等的两个角一定不是对顶角 | |
| D. | 相等的角不可能是邻补角 |
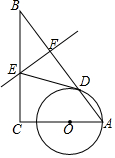 如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.


