题目内容
17.李莉在五张完全相同并且没有任何标记的卡片的一面分别写下数据-4,-1,0,3,5,将写有数据的一面朝下放置,并混合均匀.(1)随机摸起一张,求上面的数据为负数的概率;
(2)随机摸起两张,其中一张表示x,另一张表示y,求点(x,y)在直线y=-x-1上的概率;
(3)随机摸起一张,记为x,然后放回,混合均匀后再随机摸起一张,记为y,求点(x,y)是第四象限内的点的概率.
分析 (1)负数有两个,根据概率公式计算即可;
(2)先画树状图展示所有20种等可能的结果数,再判断在直线y=-x-1上的结果数,然后根据概率公式求解;
(3)先画树状图展示所有25种等可能的结果数,再判断在第四象限的结果数,然后根据概率公式求解;
解答 解:(1)上面的数据为负数的概率$\frac{2}{5}$;
(2)树状图如图所示,
一共有20种情形,点(x,y)在y=-x-1上的有4种情形,
点(x,y)在直线y=-x-1的概率为$\frac{4}{20}$=$\frac{1}{5}$;
(3)树状图如图所示,
一共有25种情形,点(x,y)在第四象限有4种情形,
点(x,y)是第四象限内的点的概率为$\frac{4}{25}$.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.也考查了一次函数图象上点的坐标特征.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列式子的变形中,正确的是( )
| A. | 由6+x=10得x=10+6 | B. | 由2(x-1)=3得2x-1=3 | ||
| C. | 由3x+5=4x得3x-4x=-5 | D. | 由8x=4-3x得8x-3x=4 |
8.已知k为任意实数,随着k的变化,抛物线y=x2-2(k-1)x+k2-3的顶点随之运动,则顶点运动时经过的路径与两条坐标轴围成图形的面积是( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
2.若a+b+c=0,那么关于x的方程ax2+bx+c=0(a≠0)必有一根是( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 0 |
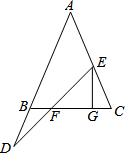 如图,∠ABC=∠C,点E在线段AC上,D在AB的延长线上,且有BD=CE,连接DE交BC于F,过E作FG⊥BC于G.试说明线段EF、FG、CG之间的数量关系.
如图,∠ABC=∠C,点E在线段AC上,D在AB的延长线上,且有BD=CE,连接DE交BC于F,过E作FG⊥BC于G.试说明线段EF、FG、CG之间的数量关系.