题目内容
已知点A(x1,y1),B(x2,y2)在抛物线y=2x2-4x+1上,且x1>x2>1,则y1 y2(填“>”、“=”或“<”).
考点:二次函数图象上点的坐标特征
专题:
分析:抛物线y=2x2-4x+1的对称轴为x=-
=-
=1,二次函数图象的性质a>0时,抛物线开口向上,在对称轴的右侧y随x的增大而增大,且x1>x2>1,故y1>y2.
| b |
| 2a |
| -4 |
| 2×2 |
解答:解:∵对称轴为x=-
=-
=1,且x1>x2>1,
∴y1与y2的大小关系是y1>y2.
故答案为>.
| b |
| 2a |
| -4 |
| 2×2 |
∴y1与y2的大小关系是y1>y2.
故答案为>.
点评:本题考查了二次函数y=ax2+bx+c(a≠0)的性质,当二次项系数a>0时,在对称轴的左边,y随x的增大而减小,在对称轴的右边,y随x的增大而增大;a<0时,在对称轴的左边,y随x的增大而增大,在对称轴的右边,y随x的增大而减小.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
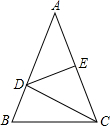 如图,△ABC中,AB=AC,D是AB边上的一点,DE垂直平分AC,∠A=40°,求∠BDC的度数.
如图,△ABC中,AB=AC,D是AB边上的一点,DE垂直平分AC,∠A=40°,求∠BDC的度数. 如图,△ABC≌△AED,∠B=40°,∠EAB=30°,∠ACB=45°,∠D=
如图,△ABC≌△AED,∠B=40°,∠EAB=30°,∠ACB=45°,∠D= 如果将点P绕定点M绕转180°后与点Q重合,那么称点P与点Q关于点M对称,定点M叫做对称中心.此时,M是线段PQ的中点.
如果将点P绕定点M绕转180°后与点Q重合,那么称点P与点Q关于点M对称,定点M叫做对称中心.此时,M是线段PQ的中点.