题目内容
1.若(x2-2x-3)(ax+b)的展开式中不含有x项且二次项的系数为1,则b=$\frac{3}{7}$.分析 根据多项式乘多项式的法则把原式变形,根据题意列出方程组,解方程组即可.
解答 解:(x2-2x-3)(ax+b)
=ax3+bx2-2ax2-2bx-3ax-3b
=ax3+(b-2a)x2-(2b+3a)x-3b,
由题意得,$\left\{\begin{array}{l}{b-2a=1}\\{2b+3a=0}\end{array}\right.$,
解得,a=-$\frac{2}{7}$,b=$\frac{3}{7}$,
故答案为:$\frac{3}{7}$.
点评 本题考查的是多项式乘多项式,多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.

练习册系列答案
相关题目
12.下列计算正确的是( )
| A. | $\sqrt{5}-\sqrt{3}=2$ | B. | $\sqrt{\frac{2}{7}}+\sqrt{\frac{5}{7}}=1$ | C. | $\frac{\sqrt{4}}{2}=2$ | D. | $\sqrt{2x}+\frac{1}{3}\sqrt{2x}=\frac{4}{3}\sqrt{2x}$ |
10.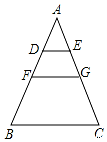 如图在△ABC中,DE∥FG∥BC,AD:AF:AB=1:3:6,则S△ADE:S四边形DEGF:S四边形FGCB=( )
如图在△ABC中,DE∥FG∥BC,AD:AF:AB=1:3:6,则S△ADE:S四边形DEGF:S四边形FGCB=( )
 如图在△ABC中,DE∥FG∥BC,AD:AF:AB=1:3:6,则S△ADE:S四边形DEGF:S四边形FGCB=( )
如图在△ABC中,DE∥FG∥BC,AD:AF:AB=1:3:6,则S△ADE:S四边形DEGF:S四边形FGCB=( )| A. | 1:8:27 | B. | 1:4:9 | C. | 1:8:36 | D. | 1:9:36 |
11. a,b,c在数轴上的位置如图所示,则下列说法正确的是( )
a,b,c在数轴上的位置如图所示,则下列说法正确的是( )
 a,b,c在数轴上的位置如图所示,则下列说法正确的是( )
a,b,c在数轴上的位置如图所示,则下列说法正确的是( )| A. | a,b,c是负数 | B. | a,b,c是正数 | ||
| C. | a,b是负数,c是正数 | D. | a是负数,b,c是正数 |