Question

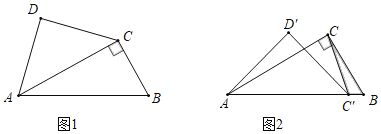
【题目】一副三角板如图1放置（有一条边重合），如图2把含45°的直角三角板ACD绕点A顺时针旋转30°，得到△AC′D′，若BC＝2，则△BCC′的面积为（　　）

A.2﹣3B.3﹣C.4﹣6D.6﹣2

Answer 1

【答案】A

【解析】

由直角三角形的性质可得AB＝2BC＝4，AC＝BC＝2，由面积法可求CH的长，由旋转的性质可得AC'＝AC＝2，由三角形面积公式可求解．

解：过点C作CH⊥AB于H，

∵BC＝2，∠CAB＝30°，∠ACB＝90°，

∴AB＝2BC＝4，AC＝BC＝2，

∵S△ABC＝AC×BC＝AB×CH，

∴CH＝＝，

∵将直角三角板ACD绕点A顺时针旋转30°，得到△AC′D′，

∴AC'＝AC＝2，

∴BC'＝AB﹣AC'＝4﹣2，

∴△BCC′的面积＝×（4﹣2）×＝2﹣3，

故选：A．