Question

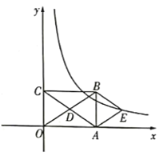
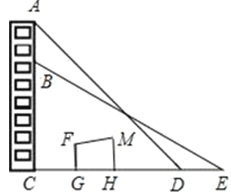
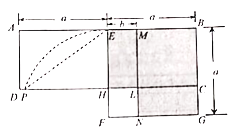
【题目】如图，在矩形ABCD中，E为AB中点，以BE为边作正方形BEFG，边EF交CD于点H，在边BE上取点M使BM＝BC，作MN∥BG交CD于点L，交FG于点N．欧儿里得在《几何原本》中利用该图解释了．现以点F为圆心，FE为半径作圆弧交线段DH于点P，连结EP，记△EPH的面积为S1，图中阴影部分的面积为S2．若点A，L，G在同一直线上，则的值为（ ）

A.B.C.D.

Answer 1

【答案】C

【解析】

连接AG，由△ADL∽△GCL列出比例式，整理可得a=3b，然后分别用含b的式子表示出，即可解决问题.

解：连接AG，点A，L，G在同一直线上，

∴PF=a，AD=a-b，DL=a+b，CL=a-b，CG=b，

∵AD∥CG，∴△ADL∽△GCL，

∴，即，

整理可得：a=3b，

PH=，

∴，

，

∴，

故选C.