题目内容
10.如果不论k为何值,x=-1总是关于x的方程$\frac{kx+a}{2}$=-$\frac{x+bk}{3}$的解,求ab的值.分析 把x=-1代入方程得到(-3+2b)k+3a-2=0,根据不论k为何值,x=-1总是关于x的方程$\frac{kx+a}{2}$=-$\frac{x+bk}{3}$的解,得到-3+2b=0,求得b,进一步求得a,再代入计算即可求解.
解答 解:把x=-1代入方程,得
$\frac{-k+a}{2}$=-$\frac{-1+bk}{3}$.
3(-k+a)=-2(-1+bk),
-3k+3a=2-2bk,
(-3+2b)k+3a-2=0,
∵不论k为何值,x=-1总是关于x的方程$\frac{kx+a}{2}$=-$\frac{x+bk}{3}$的解,
∴-3+2b=0,
解得b=$\frac{3}{2}$,
∴3a-2=0,
解得a=$\frac{2}{3}$,
∴ab=$\frac{3}{2}$×$\frac{2}{3}$=1.
点评 本题考查一元一次方程的解,灵活变换题目的条件是解决本题的关键.本题难点是得到a,b的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.下列计算正确的是( )
| A. | 6x2•3xy=9x3y | B. | (2ab2)•(-3ab)=-a2b3 | C. | (mn)2•(-m2n)=-m3n3 | D. | (-3x2y)(-3xy)=9x3y2 |
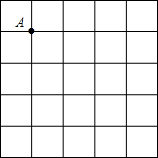 如图,在5×5的正方形网格中,每个小正方形的边长都为1.请在所给网格中按下列要求画出图形.
如图,在5×5的正方形网格中,每个小正方形的边长都为1.请在所给网格中按下列要求画出图形. 已知菱形ABCD中,E、F分别是CB、CD上的点,且BE=DF.
已知菱形ABCD中,E、F分别是CB、CD上的点,且BE=DF.