Question

10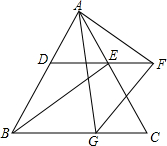．如图，在等边三角形ABC中，点D，E分别是在边AB，AC上，DE∥BC，点F在DE的延长线上，且FC=EC．
（1）求证：△ADF≌△EAB；
（2）点G在BC边上，若FG∥EB，求∠AGF的度数．

Answer 1

分析 （1）先证△BDE≌△FEA，得出BE=FA，∠BED=∠FAE，再利用角的关系，找到∠AEB=∠DAF，从而能够证出△ADF≌△EAB；
（2）利用（1）中的三角形全等，得出BE=FA，∠DBE=∠EFA，利用角的关系找到∠AFG=60°，借助两组对边平行的四边形为平行四边形，可得出BE=GF，等腰三角形中顶角为60°则此三角形为等边三角形，得出结论．

解答 （1）证明：连接FC，如图，

∵DE∥BC，且△ABC为等边三角形，
∴∠ADE=∠ABC=60°，∠AED=∠ACB=60°，AB=BC=CA
∴△ADE为等边三角形，AD=DE=AE，
∵FC=EC，∠CEF=∠AED=60°（对顶角），
∴△ECF为等边三角形，EC=FC=EF，
∵BD=AB-AD，EC=AC-AE，
∴BD=CE=EF，
∠BDE=180°-∠ADE=120°，∠FEA=180°-∠AED=120°，
∴∠BDE=∠FEA，
在△BDE和△FEA中，$\left\{\begin{array}{l}{BD=FE}\\{∠BDE=∠FEA}\\{DE=EA}\end{array}\right.$，
∴△BDE≌△FEA，
∴BE=FA，∠BED=∠FAE，
∠AEB=∠AED+∠BED，∠DAF=∠DAE+∠FAE，
∴∠AEB=∠DAF，
在△ADF和△EAB中，$\left\{\begin{array}{l}{DA=AE}\\{∠AEB=∠DAF}\\{BE=FA}\end{array}\right.$，
∴△ADF≌△EAB（SAS），
证毕．
（2）解：∵EF∥BG，FG∥EB，
∴四边形BGFE为平行四边形，
∴BE=GF，∠EBG=∠EFG，
∵△BDE≌△FEA，
∴∠DBE=∠EFA，
∵∠DBE+∠EBG=∠ABC=60°，
∴∠EFA+∠EFG=60°，
∵BE=FA=GF，
∴△AGF为等边三角形，
∴∠AGF=60°．

点评 本题考查了全等三角形的判定和性质定理以及平行四边形的判定和性质定理，解题的关键是结合图形，一步步的寻找相等的量．