题目内容
18.如图1,已知二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为-$\frac{8}{3}$,直线l的解析式为y=x.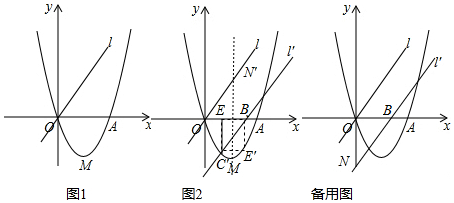
(1)求二次函数的解析式;
(2)直线l沿x轴向右平移,得直线l′,l′与线段OA相交于点B,与x轴下方的抛物线相交于点C,过点C作CE⊥x轴于点E,把△BCE沿直线l′折叠,当点E恰好落在抛物线上点E′时(图2),求直线l′的解析式;
(3)在(2)的条件下,l′与y轴交于点N,把△BON绕点O逆时针旋转135°得到△B′ON′,P为l′上的动点,当△PB′N′为等腰三角形时,求符合条件的点P的坐标.
分析 (1)由题意抛物线的顶点坐标为(2,-$\frac{8}{3}$),设抛物线的解析式为y=a(x-2)2-$\frac{8}{3}$,把(0,0)代入得到a=$\frac{2}{3}$,即可解决问题;
(2)如图1中,设E(m,0),则C(m,$\frac{2}{3}$m2-$\frac{8}{3}$m),B(-$\frac{2}{3}$m2+$\frac{11}{3}$m,0),由E、B关于对称轴对称,可得$\frac{m+(-\frac{2}{3}{m}^{2}+\frac{11}{3}m)}{2}$=2,由此即可解决问题;
(3)分两种情形求解即可①当P1与N重合时,△P1B′N′是等腰三角形,此时P1(0,-3).②当N′=N′B′时,设P(m,m-3),列出方程解方程即可;
解答 解:(1)由题意抛物线的顶点坐标为(2,-$\frac{8}{3}$),设抛物线的解析式为y=a(x-2)2-$\frac{8}{3}$,
把(0,0)代入得到a=$\frac{2}{3}$,
∴抛物线的解析式为y=$\frac{2}{3}$(x-2)2-$\frac{8}{3}$,即y=$\frac{2}{3}$x2-$\frac{8}{3}$x.
(2)如图1中,设E(m,0),则C(m,$\frac{2}{3}$m2-$\frac{8}{3}$m),B(-$\frac{2}{3}$m2+$\frac{11}{3}$m,0),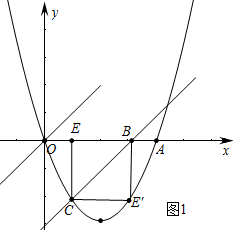
∵E′在抛物线上,易知四边形EBE′C是正方形,抛物线的对称轴也是正方形的对称轴,
∴E、B关于对称轴对称,
∴$\frac{m+(-\frac{2}{3}{m}^{2}+\frac{11}{3}m)}{2}$=2,
解得m=1或6(舍弃),
∴B(3,0),C(1,-2),
∴直线l′的解析式为y=x-3.
(3)如图2中,
①当P1与N重合时,△P1B′N′是等腰三角形,此时P1(0,-3).
②当N′=N′B′时,设P(m,m-3),
则有(m-$\frac{3\sqrt{2}}{2}$)2+(m-3-$\frac{3}{2}$$\sqrt{2}$)2=(3$\sqrt{2}$)2,
解得m=$\frac{3\sqrt{2}+3-3\sqrt{3}}{2}$或$\frac{3\sqrt{2}+3+3\sqrt{3}}{2}$,
∴P2($\frac{3\sqrt{2}+3-3\sqrt{3}}{2}$,$\frac{3\sqrt{2}-3-3\sqrt{3}}{2}$),P3($\frac{3\sqrt{2}+3+3\sqrt{3}}{2}$,$\frac{3\sqrt{2}-3+3\sqrt{3}}{2}$).
综上所述,满足条件的点P坐标为(0,-3)或($\frac{3\sqrt{2}+3-3\sqrt{3}}{2}$,$\frac{3\sqrt{2}-3-3\sqrt{3}}{2}$)或($\frac{3\sqrt{2}+3+3\sqrt{3}}{2}$,$\frac{3\sqrt{2}-3+3\sqrt{3}}{2}$).
点评 本题考查二次函数综合题、待定系数法、等腰三角形的判定和性质、两点间距离公式等知识,解题的关键是学会用分类讨论的思想思考问题,学会根据方程,属于中考压轴题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 该方程有两个不相等的实数根 | B. | 该方程有两个相等的实数根 | ||
| C. | 该方程有实数根 | D. | 该方程没有实数根 |
| A. | a2+a3=a5 | B. | 6a5÷(-2a3)=-3a2 | C. | (-a3)2=-a6 | D. | (a-b)2=a2-b2 |
| A. | a2•a3 | B. | (-a2)3 | C. | (a2)3 | D. | a12-a6 |
| A. | (-2ab)•(-3ab)3=-54a4b4 | B. | 5x2•(3x3)2=15x12 | ||
| C. | (-0.1b)•(-10b2)3=-b7 | D. | (3×10n)($\frac{1}{3}$×10n)=102n |
 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
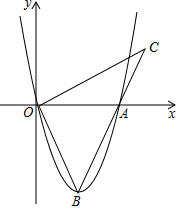 如图,抛物线y=ax2-4x的图象与x轴的一个交点为A(6,0),点B为抛物线的顶点,连结OB、AB,作OC⊥OB交BA的延长线于点C.
如图,抛物线y=ax2-4x的图象与x轴的一个交点为A(6,0),点B为抛物线的顶点,连结OB、AB,作OC⊥OB交BA的延长线于点C. 如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买5千克这种苹果比分五次购买1千克这种苹果可节省( )元.
如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买5千克这种苹果比分五次购买1千克这种苹果可节省( )元.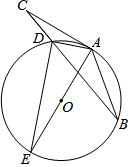 如图,在△ABC中,点D为BC上一点,过A,B,D三点作⊙O,AE是⊙O的直径,AC是⊙O的切线,AD=DC,连结DE.
如图,在△ABC中,点D为BC上一点,过A,B,D三点作⊙O,AE是⊙O的直径,AC是⊙O的切线,AD=DC,连结DE.