题目内容
12. 已知:如图△ABC是等边三角形,D、E分别是BC,AC上两点且BD=CE,以AD为边在AC一侧作等边△ADF.求证:EF∥BC.
已知:如图△ABC是等边三角形,D、E分别是BC,AC上两点且BD=CE,以AD为边在AC一侧作等边△ADF.求证:EF∥BC.
分析 连接CF,根据等边三角形的性质求得AB=AC,AD=AF,∠BAD=∠CAF,然后证得△BAD和△CAF全等,得出∠ACF=∠ABD=60°,BD=CF,进而证得△CEF是等边三角形,得出∠CEF=∠ACB=60°,即可证得结论.
解答 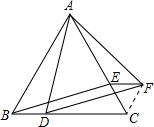 证明:连接CF,
证明:连接CF,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ACB=∠ABC=60°,
∵△ADF是等边三角形,
∴AD=AF,∠DAF=60°,
∴∠BAC=∠DAF=60°,
∴∠BAC-∠DAC=∠DAF-∠DAC,即∠BAD=∠CAF,
在△BAD和△CAF中
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$,
∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=60°,BD=CF,
∵BD=CE,
∴CF=CE,
∴△CEF是等边三角形,
∴∠CEF=60°,
∴∠CEF=∠ACB=60°,
∴EF∥BC.
点评 本题考查了等边三角形的判定和性质,三角形全等的判定和性质,平行线的判定等,证得△CEF是等边三角形是解题的关键.

练习册系列答案
相关题目
1. 如图,点B、D、C、E在同一直线上,△ABC经过怎样的平移可得到△FDE( )
如图,点B、D、C、E在同一直线上,△ABC经过怎样的平移可得到△FDE( )
 如图,点B、D、C、E在同一直线上,△ABC经过怎样的平移可得到△FDE( )
如图,点B、D、C、E在同一直线上,△ABC经过怎样的平移可得到△FDE( )| A. | 沿射线BD的方向移动BD长 | B. | 沿射线EC的方向移动CD长 | ||
| C. | 沿射线EC的方向移动DB长 | D. | 沿射线BD的方向移动DC长 |
2.下列语句错误的是( )
| A. | 实数可分为有理数和无理数 | B. | 无理数可分为正无理数和负无理数 | ||
| C. | 无理数都是无限小数 | D. | 无限小数都是无理数 |
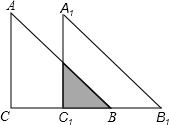 如图,Rt△ABC中∠C=90°,AC=BC=4,将△ABC沿CB方向移动到△A1B1C1的位置,
如图,Rt△ABC中∠C=90°,AC=BC=4,将△ABC沿CB方向移动到△A1B1C1的位置, 如图,每个网格都是边长为1个单位的小正方形,△ABC的每个顶点都在网格的格点上,且∠C=90°,AC=3,BC=4.
如图,每个网格都是边长为1个单位的小正方形,△ABC的每个顶点都在网格的格点上,且∠C=90°,AC=3,BC=4.