题目内容
在平面直角坐标系Oxy中,抛物线y=x2-4x+k(k是常数)与x轴相交于A、B两点(B在A的右边),与y轴相交于C点.
(1)求k的取值范围;
(2)若△OBC是等腰直角三角形,求k的值.
(1)求k的取值范围;
(2)若△OBC是等腰直角三角形,求k的值.
考点:抛物线与x轴的交点,等腰直角三角形
专题:
分析:(1)由抛物线的图象和x轴有两个交点可知:△>0,进而可求出k的取值范围;
(2)易求C的坐标为(0,k),若△OBC是等腰直角三角形则|k|2-4|k|+k=0,即可求出k的值.
(2)易求C的坐标为(0,k),若△OBC是等腰直角三角形则|k|2-4|k|+k=0,即可求出k的值.
解答:解:(1)依题意,(-4)2-4k>0,
解不等式得,k<4,
所以k的取值范围是k<4;
(2)依题意,C(0,k),
∴B(|k|,0),
∴|k|2-4|k|+k=0,
∴k>0时,k2-3k=0,解得k=3;
k<0时,k2+5k=0,解得k=-5.
解不等式得,k<4,
所以k的取值范围是k<4;
(2)依题意,C(0,k),
∴B(|k|,0),
∴|k|2-4|k|+k=0,
∴k>0时,k2-3k=0,解得k=3;
k<0时,k2+5k=0,解得k=-5.
点评:本题考查了抛物线和x轴交点的问题,一般求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
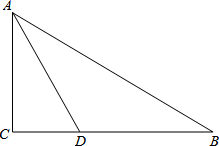 如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的平分线.
如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的平分线. 如图,AC是⊙O的切线,BC是直径,AB交⊙O于点D,∠A=50°,那么∠COD=
如图,AC是⊙O的切线,BC是直径,AB交⊙O于点D,∠A=50°,那么∠COD=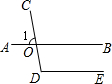 已知:AB、CD相交于点O,∠1=80°,如果DE∥AB,求∠D的度数为
已知:AB、CD相交于点O,∠1=80°,如果DE∥AB,求∠D的度数为 小辉身高1.65米,他在体质健康卡上填写的是165厘米,其实这是度量单位引起的数值变化:以1米为度量单位,那么他的身高就是1.65个度量单位,以1厘米为度量单位,那么他的身高就是165个度量单位.
小辉身高1.65米,他在体质健康卡上填写的是165厘米,其实这是度量单位引起的数值变化:以1米为度量单位,那么他的身高就是1.65个度量单位,以1厘米为度量单位,那么他的身高就是165个度量单位.