题目内容
 如图.Rt△ABC内接于⊙O,BC为直径,AB=4,AC=3,D是
如图.Rt△ABC内接于⊙O,BC为直径,AB=4,AC=3,D是 |
| AB |
| CE |
| DE |
考点:垂径定理,三角形中位线定理,圆周角定理,相似三角形的判定与性质
专题:
分析:利用垂径定理的推论得出DO⊥AB,AF=BF,进而得出DF的长和△DEF∽△CEA,再利用相似三角形的性质求出即可.
解答:解:连接DO,交AB于点F,
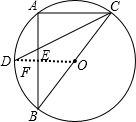
∵D是
的中点,
∴DO⊥AB,AF=BF,
∵AB=4,
∴AF=BF=2,
∴FO是△ABC的中位线,AC∥DO,
∵BC为直径,AB=4,AC=3,
∴BC=5,
∴DO=2.5,
∴DF=2.5-1.5=1,
∵AC∥DO,
∴△DEF∽△CEA,
∴
=
,
∴
=
=3.
故答案为:3.

∵D是
 |
| AB |
∴DO⊥AB,AF=BF,
∵AB=4,
∴AF=BF=2,
∴FO是△ABC的中位线,AC∥DO,
∵BC为直径,AB=4,AC=3,
∴BC=5,
∴DO=2.5,
∴DF=2.5-1.5=1,
∵AC∥DO,
∴△DEF∽△CEA,
∴
| CE |
| DE |
| AC |
| DF |
∴
| CE |
| DE |
| 3 |
| 1 |
故答案为:3.
点评:此题主要考查了垂径定理的推论以及相似三角形的判定与性质,根据已知得出△DEF∽△CEA是解题关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
如图,第①个图有2个相同的小正方形,第②个图有6个相同的小正方形,第③个图有12个相同的小正方形,…,按此规律,那么第15个图中小正方形的个数是( )
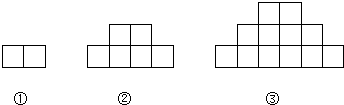

| A、225 | B、240 |
| C、30 | D、255 |
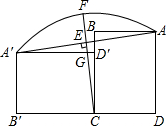 如图,将矩形ABCD向左绕点C推倒,恰好D落在BC上D′处,得到矩形A′B′C′D′,作CE⊥AA′交
如图,将矩形ABCD向左绕点C推倒,恰好D落在BC上D′处,得到矩形A′B′C′D′,作CE⊥AA′交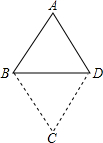 如图,将等边△ABD沿BD中点旋转180°得到△BDC.现给出下列命题:
如图,将等边△ABD沿BD中点旋转180°得到△BDC.现给出下列命题: 在Rt△ABC中,∠ABC=90°,D为AC上一点,E是BD中点,∠1=∠2,求证:∠ADB=2∠ABD.
在Rt△ABC中,∠ABC=90°,D为AC上一点,E是BD中点,∠1=∠2,求证:∠ADB=2∠ABD.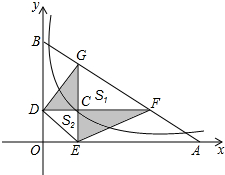 如图,已知动点C在函数
如图,已知动点C在函数 如图,∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?为什么?
如图,∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?为什么?