题目内容
10.从南京到某市可乘坐普通列车,行驶路程是520千米;也可乘坐高铁,行驶路程是400千米.已知高铁的平均速度是普通列车平均速度的2.5倍,且从南京到该市乘坐高铁比乘坐普通列车要少用3小时.求高铁行驶的平均速度.分析 设普通列车的平均速度为x千米/时,则高铁的平均速度是2.5x千米/时,根据题意可得,乘坐高铁行驶400千米比乘坐普通列车行驶520千米少用3小时,据此列方程求解.
解答 解:设普通列车的平均速度为x千米/时,
则高铁的平均速度是2.5x千米/时,
依题意,得$\frac{400}{2.5x}$+3=$\frac{520}{x}$,
解得:x=120,
经检验,x=120是原方程的解,且符合题意,
则2.5x=300.
答:高铁行驶的平均速度是300千米/时.
点评 本题考查了分式方程的应用,解答本题案的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解,注意检验.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
20.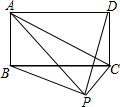 已知矩形ABCD,当点P在图中的位置时,则有结论( )
已知矩形ABCD,当点P在图中的位置时,则有结论( )
 已知矩形ABCD,当点P在图中的位置时,则有结论( )
已知矩形ABCD,当点P在图中的位置时,则有结论( )| A. | S△PBC=S△PAC+S△PCD | B. | S△PBC=S△PAC-S△PCD | ||
| C. | S△PAB+S△PCD=$\frac{1}{2}$S矩形ABCD | D. | S△PAB+S△PCD<$\frac{1}{2}$S矩形ABCD |
18.解不等式组$\left\{\begin{array}{l}{2(x-1)≥x+1}\\{x-2>\frac{1}{3}(2x-1)}\end{array}\right.$,并在数轴上表示出解集.
15.函数y=$\sqrt{x-2}$中,自变量x的取值范围是( )
| A. | x≠2 | B. | x≥2 | C. | x>2 | D. | x≥-2 |
19.函数y=$\sqrt{x-2}$,自变量x的取值范围是( )
| A. | x>2 | B. | x<2 | C. | x≥2 | D. | x≤2 |
20.下列所给图形中,既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |