题目内容
20. 如图,已知平面内A、B、C三点.
如图,已知平面内A、B、C三点.(1)作直线AB,射线CB,线段AC.
(2)找出线段AB的中点O.
(3)若AB=10,在直线AB上有一点P,且AP=2,求线段OP的长.
分析 (1)根据直线、线段和射线的画法按要求画出图形;(2)分别以A、B为圆心大于$\frac{1}{2}$AB为半径画圆,连接两交点交AB于点O;(3)点P在线段AB上或在射线BA上.
解答 解:(1)(2)如图
(3)∵O为AB中点,
∴AO=$\frac{1}{2}$AB=$\frac{1}{2}$×10=5,
当P在线段AB上时OP=OA-AP=5-2=3,
当P在射线BA上时OP=OA+AP=5+2=7.
点评 本题考查了直线、射线、线段的定义以及表示方法:直线用一个小写字母表示,如:直线l,或用两个大些字母(直线上的)表示,如直线AB;射线是直线的一部分,用一个小写字母表示,如:射线l;用两个大写字母表示,端点在前,如:射线OA;线段是直线的一部分,用一个小写字母表示,如线段a;用两个表示端点的字母表示,如:线段AB(或线段BA);根据中点的定义和P点的位置得出两种结果是解题的关键.

练习册系列答案
相关题目
8.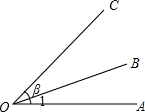 如图,下列表示角的说法,错误的是( )
如图,下列表示角的说法,错误的是( )
 如图,下列表示角的说法,错误的是( )
如图,下列表示角的说法,错误的是( )| A. | ∠AOC也可用∠O表示 | B. | ∠1与∠AOB表示同一个角 | ||
| C. | ∠β表示的是∠BOC | D. | ∠AOB和∠BOC都不能用∠O表示 |
15.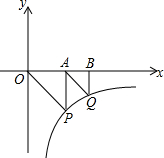 如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=-$\frac{9}{x}$(x>0)的图象上,直角顶点A、B均在x轴上,则点B的坐标为( )
如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=-$\frac{9}{x}$(x>0)的图象上,直角顶点A、B均在x轴上,则点B的坐标为( )
 如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=-$\frac{9}{x}$(x>0)的图象上,直角顶点A、B均在x轴上,则点B的坐标为( )
如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数y=-$\frac{9}{x}$(x>0)的图象上,直角顶点A、B均在x轴上,则点B的坐标为( )| A. | (6,0) | B. | (9,0) | C. | ($\frac{3+3\sqrt{5}}{2}$,0) | D. | ($\frac{3\sqrt{2}+3}{2}$,0) |
5.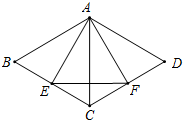 如图,已知等边三角形AEF的两个顶点E、F都在菱形ABCD的边上,EF⊥AC,下列结论,①CE=CF;②∠BAE=∠DAF;③BE=EC;④三角形AEF的面积等于菱形ABCD的面积的一半,其中正确的个数是( )
如图,已知等边三角形AEF的两个顶点E、F都在菱形ABCD的边上,EF⊥AC,下列结论,①CE=CF;②∠BAE=∠DAF;③BE=EC;④三角形AEF的面积等于菱形ABCD的面积的一半,其中正确的个数是( )
 如图,已知等边三角形AEF的两个顶点E、F都在菱形ABCD的边上,EF⊥AC,下列结论,①CE=CF;②∠BAE=∠DAF;③BE=EC;④三角形AEF的面积等于菱形ABCD的面积的一半,其中正确的个数是( )
如图,已知等边三角形AEF的两个顶点E、F都在菱形ABCD的边上,EF⊥AC,下列结论,①CE=CF;②∠BAE=∠DAF;③BE=EC;④三角形AEF的面积等于菱形ABCD的面积的一半,其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.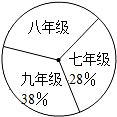 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表(1)是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是( )
阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表(1)是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是( )
 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表(1)是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是( )
阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表(1)是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是( )| 图书种类 | 频数 | 频率 |
| 科普知识 | 840 | B |
| 名人传记 | 816 | 0.34 |
| 漫画丛书 | A | 0.25 |
| 其它 | 144 | 0.06 |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
10.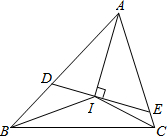 我们知道,任何一个三角形的三条内角平分线相交于一点.如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.
我们知道,任何一个三角形的三条内角平分线相交于一点.如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.
(1)请你通过计算,填写表格.
(2)从表中你发现了∠BIC与∠BDI之间有何数量关系,请写出来,并说明其中的道理,它们的关系是∠BIC=∠BDI.
 我们知道,任何一个三角形的三条内角平分线相交于一点.如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.
我们知道,任何一个三角形的三条内角平分线相交于一点.如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.(1)请你通过计算,填写表格.
(2)从表中你发现了∠BIC与∠BDI之间有何数量关系,请写出来,并说明其中的道理,它们的关系是∠BIC=∠BDI.
| ∠BAC的度数 | 60° | 100° |
| ∠BIC的度数 | 120° | 140° |
| ∠BDI的度数 | 120° | 140° |
11.($\frac{2}{3}$)1992×(1.5)1991×(-1)1993的结果是( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
 如图所示,一块长为18m,宽为12m的草地上有一条宽为2m的曲折的小路,求这块草地的绿地面积.
如图所示,一块长为18m,宽为12m的草地上有一条宽为2m的曲折的小路,求这块草地的绿地面积.