题目内容
9.如图1,点B是线段AC的中点,以线段BC为边作矩形BCDE,点P是线段AC上一动点,连接DP,过点D作DP的垂线,交射线BE于点F,点P从点A出发,沿AC方向运动,当点P和点C重合时运动停止,设线段AP的长为x,△PBF的面积为S,S关于x的函数图象如图2所示(其中0≤x≤2,2<x≤m时,函数的解析式不同).(1)填空:CD的长度为3;
(2)求S关于x的函数关系式,并写出x的取值范围.
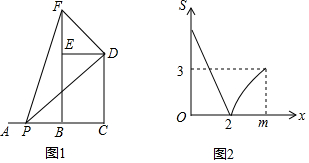
分析 (1)根据图1和图2中面积为0的情况可知:AB=BC=2,则AC=4,由图2中当x=m时,S=3,代入可求得CD的长;
(2)先求当P与A重合时,EF的长,即DG的长,求出此时S的值,即图2中M的坐标,由图2可知MN是一次函数,利用待定系数法可求MN的解析式,也可以利用图1求0≤x≤2时,S与x的函数关系式,当2≤x≤4时,利用相似求DG的长,可以表示S的值.
解答 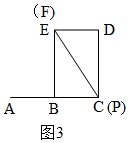 解:(1)由图1知:P与B重合时,S=0;
解:(1)由图1知:P与B重合时,S=0;
由图2知:x=2时,S=0;
∴AB=BC=2,
∴AC=4,
∴m=4,
当P与C重合时,F与E重合,如图3,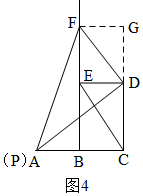
∴S=S△PDF=$\frac{1}{2}$DE•CD=3,
$\frac{1}{2}$×2×CD=3,
CD=3,
故答案为:3;
(2)当x=0时,如图4,P与A重合,
过F作FG⊥CD,交CD的延长线于G,
∵FD⊥PD,
∴∠FDP=90°,
∴∠FDG+∠ADC=90°,
∵∠G=90°,
∴∠FDG+∠DFG=90°,
∴∠ADC=∠DFG,
∵∠G=∠ACD=90°,
∴△ADC∽△DFG,
∴$\frac{AC}{DG}=\frac{CD}{FG}$,
∴$\frac{4}{DG}=\frac{3}{2}$,
∴DG=$\frac{8}{3}$;
由勾股定理得:AD=$\sqrt{{3}^{2}+{4}^{2}}$=5,DF=$\sqrt{{2}^{2}+(\frac{8}{3})^{2}}$=$\frac{10}{3}$,
∴当x=0时,S=$\frac{1}{2}$AB•BF=$\frac{1}{2}$×$2×(3+\frac{8}{3})$=$\frac{17}{3}$,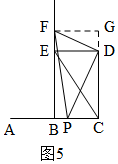
∴M(0,$\frac{17}{3}$),N(2,0),
当0≤x≤2时,设MN的解析式为:S=kx+b,
则$\left\{\begin{array}{l}{2k+b=0}\\{b=\frac{17}{3}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{17}{6}}\\{b=\frac{17}{3}}\end{array}\right.$,
∴MN的解析式为:S=-$\frac{17}{6}$x+$\frac{17}{3}$(0≤x≤2),
当2≤x≤4时,如图5,
同理得:△PDC∽△DFG,
∴$\frac{PC}{DG}=\frac{CD}{FG}$,
∴$\frac{4-x}{DG}=\frac{3}{2}$,
∴DG=$\frac{2(4-x)}{3}$,
∴S=S△FBP=$\frac{1}{2}$PB•BF,
=$\frac{1}{2}$(x-2)[3+$\frac{2(4-x)}{3}$],
=-$\frac{1}{3}{x}^{2}+\frac{7}{2}x-\frac{17}{3}$;
综上所述,S关于x的函数关系式为:S=$\left\{\begin{array}{l}{-\frac{17}{6}x+\frac{17}{3}(0≤x≤2)}\\{-\frac{1}{3}{x}^{2}+\frac{7}{2}x-\frac{17}{3}(2≤x≤4)}\end{array}\right.$.
点评 本题考查了动点问题的函数图象,此类题有难度,理解图1和图2的关系是关键,注意弄清已知中图2的3和2表示的含义,分情况讨论,利用三角形面积公式可以解决问题.

 如图,四边形ABCD是正方形,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )
如图,四边形ABCD是正方形,AE垂直于BE,且AE=6,BE=8,则阴影部分的面积是( )| A. | 66 | B. | 76 | C. | 64 | D. | 100 |
 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.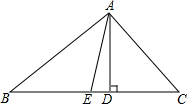 已知:如图,在△ABC中,AD是BC边上的高,AE是∠BAC平分线,∠B=30°,∠DAE=15°,
已知:如图,在△ABC中,AD是BC边上的高,AE是∠BAC平分线,∠B=30°,∠DAE=15°,