题目内容
3.已知等边三角形的边长为2,则其面积等于$\sqrt{3}$.分析 根据等边三角形三线合一的性质可得D为BC的中点,即BD=CD,在直角三角形ABD中,已知AB、BD,根据勾股定理即可求得AD的长,即可求三角形ABC的面积,即可解题.
解答 解:∵等边三角形高线即中点,AB=2,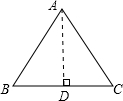
∴BD=CD=1,
在Rt△ABD中,AB=2,BD=1,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}=\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$,
故答案为$\sqrt{3}$
点评 本题考查的是等边三角形的性质,熟知等腰三角形“三线合一”的性质是解题的关键.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
14.下列各图案中是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.在下列各数中,无理数是( )
| A. | $\sqrt{4}$ | B. | 3π | C. | $\frac{22}{7}$ | D. | $\root{3}{8}$ |
2.将抛物线y=x2向左平移5个单位后得到的抛物线对应的函数解析式是( )
| A. | y=-x2+5 | B. | y=x2-5 | C. | y=(x-5)2 | D. | y=(x+5)2 |
3.若∠α与∠β互为补角,∠β是∠α的2倍,则∠α为( )
| A. | 30° | B. | 40° | C. | 60° | D. | 120° |
 甲、乙两村之间隔着两条河(如图所示),为使两村之间的行程最短,应在这两条河的什么位置各架一座桥?(作图表示)
甲、乙两村之间隔着两条河(如图所示),为使两村之间的行程最短,应在这两条河的什么位置各架一座桥?(作图表示)