题目内容
11.先化简,再求值:$\frac{{{a^2}-2a+1}}{{{a^2}-1}}$+(a-1-$\frac{a-1}{a+1}}$),其中a=2$\sqrt{2}$.分析 首先化简$\frac{{{a^2}-2a+1}}{{{a^2}-1}}$+(a-1-$\frac{a-1}{a+1}}$),然后把a=2$\sqrt{2}$代入化简后的算式,求出算式的值是多少即可.
解答 解:$\frac{{{a^2}-2a+1}}{{{a^2}-1}}$+(a-1-$\frac{a-1}{a+1}}$)
=$\frac{{(a-1)}^{2}}{(a+1)(a-1)}$+$\frac{{a}^{2}-a}{a+1}$
=$\frac{a-1}{a+1}$+$\frac{{a}^{2}-a}{a+1}$
=$\frac{{a}^{2}-1}{a+1}$
=a-1
当a=2$\sqrt{2}$时
原式=2$\sqrt{2}$-1
点评 此题主要考查了分式的化简求值问题,要熟练掌握,注意先把分式化简后,再把分式中未知数对应的值代入求出分式的值.

练习册系列答案
相关题目
4.下列判断中错误的有( )
①有两角和一边对应相等的两个三角形全等
②有两边和一角对应相等的两个三角形全等
③有两边和其中一边上的中线对应相等的两个三角形全等
④有一边对应相等的两个等边三角形全等.
①有两角和一边对应相等的两个三角形全等
②有两边和一角对应相等的两个三角形全等
③有两边和其中一边上的中线对应相等的两个三角形全等
④有一边对应相等的两个等边三角形全等.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
6.若2m=3,2n=4,则23m+2n等于( )
| A. | 432 | B. | $\frac{9}{16}$ | C. | 11 | D. | 1 |
16.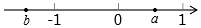 有理数a,b在数轴上对应的位置如图所示,则下列结论成立的是( )
有理数a,b在数轴上对应的位置如图所示,则下列结论成立的是( )
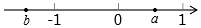 有理数a,b在数轴上对应的位置如图所示,则下列结论成立的是( )
有理数a,b在数轴上对应的位置如图所示,则下列结论成立的是( )| A. | a+b>0 | B. | a-b>0 | C. | ab>0 | D. | $\frac{a}{b}>0$ |
3.若α与β互余,且α:β=3:2,那么α的度数是( )
| A. | 18° | B. | 36° | C. | 54° | D. | 108° |
