题目内容
6.(1)计算:6cos45°+($\frac{1}{3}$)-1+($\sqrt{3}$-1.73)0+|5-3$\sqrt{2}$|+42017×(-0.25)2017(2)先化简,再求值:($\frac{3}{a+1}$-a+1)÷$\frac{{a}^{2}-4a+4}{a+1}$+$\frac{4}{a-2}$-a,并从-1,0,2中选一个合适的数作为a的值代入求值.
分析 (1)根据特殊角的三角函数值、负整数指数幂、零指数幂、绝对值、幂的乘方可以解答本题;
(2)根据分式的加减法和除法可以化简题目中的式子,然后在-1,0,2中选一个使得原分式有意义的值代入即可解答本题.
解答 解:(1)6cos45°+($\frac{1}{3}$)-1+($\sqrt{3}$-1.73)0+|5-3$\sqrt{2}$|+42017×(-0.25)2017
=6×$\frac{\sqrt{2}}{2}$+3+1+5-3$\sqrt{2}$+42017×(-$\frac{1}{4}$)2017
=$3\sqrt{2}+3+1+5-3\sqrt{2}-1$
=8;
(2)($\frac{3}{a+1}$-a+1)÷$\frac{{a}^{2}-4a+4}{a+1}$+$\frac{4}{a-2}$-a
=$\frac{3-(a-1)(a+1)}{a+1}•\frac{a+1}{(a-2)^{2}}+\frac{4}{a-2}-a$
=$\frac{-(a+2)(a-2)}{(a-2)^{2}}+\frac{4}{a-2}-a$
=$\frac{-a-2}{a-2}+\frac{4}{a-2}-a$
=$\frac{-(a-2)}{a-2}-a$
=-a-1,
当a=0时,原式=-0-1=-1.
点评 本题考查分式的化简求值、实数的运算、殊角的三角函数值、负整数指数幂、零指数幂、绝对值、幂的乘方,解答本题的关键是明确它们各自的计算方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.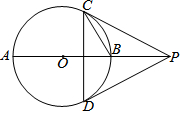 如图,AB是⊙O的直径,弦CD⊥AB,过点C作⊙O的切线与AB的延长线交于点P.若∠BCD=32°,则∠CPD的度数是( )
如图,AB是⊙O的直径,弦CD⊥AB,过点C作⊙O的切线与AB的延长线交于点P.若∠BCD=32°,则∠CPD的度数是( )
 如图,AB是⊙O的直径,弦CD⊥AB,过点C作⊙O的切线与AB的延长线交于点P.若∠BCD=32°,则∠CPD的度数是( )
如图,AB是⊙O的直径,弦CD⊥AB,过点C作⊙O的切线与AB的延长线交于点P.若∠BCD=32°,则∠CPD的度数是( )| A. | 64° | B. | 62° | C. | 58° | D. | 52° |
1.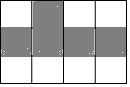 如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是( )
如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是( )
 如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是( )
如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是( )| A. | $\frac{4}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{2}{7}$ | D. | $\frac{1}{7}$ |
15.某机器人公司为扩大经营,决定购进6台机器用于生产某种小机器人.现有甲、乙两种机器供选择,其中每台机器的价格和日生产量如下表所示.经过预算,本次购买机器的费用不能超过34万元.
(1)按要求该公司有几种购买方案?
(2)若该公司购进的6台机器的日生产量不能少于380个,那么为了节约资金,应选择哪种购买方案?
| 甲种机器 | 乙种机器 | |
| 价格/(万元/台) | 5 | 7 |
| 每台机器的日生产量/个 | 60 | 100 |
(2)若该公司购进的6台机器的日生产量不能少于380个,那么为了节约资金,应选择哪种购买方案?

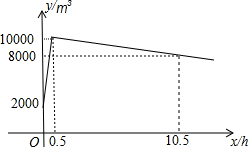 星期天8:00一8:30,燃气公司给平安加气站的储气罐注入天然气.之后,一位工作人员以每车20m3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(m3)与时间x(h)的函数关系如图所示.
星期天8:00一8:30,燃气公司给平安加气站的储气罐注入天然气.之后,一位工作人员以每车20m3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(m3)与时间x(h)的函数关系如图所示.