题目内容
【题目】在平面直角坐标系中，点
，
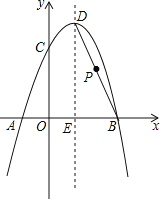
，将直线
平移与双曲线
在第一象限的图象交于
、
两点．
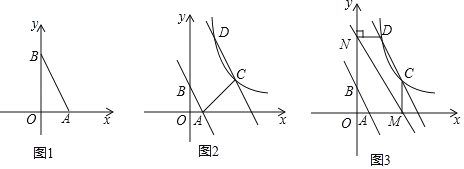
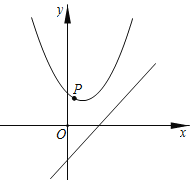
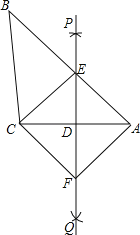
（1）如图1，将
绕
逆时针旋转
得
与对应，
与对应)，在图1中画出旋转后的图形并直接写出
、坐标；
（2）若
，
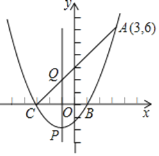
①如图2，当
时，求
的值；
②如图3，作
轴于点
，
轴于点
，直线
与双曲线
有唯一公共点时，的值为 ．
【答案】（1）作图见解析，
，
；（2）①k=6；②
．
【解析】
（1）根据题意，画出对应的图形，根据旋转的性质可得
，
，从而求出点E、F的坐标；
（2）过点
作
轴于
，过点
作
轴于
，过点作
于
，根据相似三角形的判定证出
，列出比例式，设
，根据反比例函数解析式可得
（Ⅰ）；
①根据等角对等边可得
，可列方程
(Ⅱ)，然后联立方程即可求出点D的坐标，从而求出k的值；
②用m、n表示出点M、N的坐标即可求出直线MN的解析式，利于点D和点C的坐标即可求出反比例函数的解析式，联立两个解析式，令△=0即可求出m的值，从而求出k的值．
解：（1）
点
，
，
，
，
如图1，
由旋转知，
，，，
点
在
轴正半轴上，点
在
轴负半轴上，
，；
（2）过点作轴于，过点作轴于，过点作于，
，
，
，
，
，
，
，
，
，
，
，，
，
，
，
，
设，
，
，
，
点，在双曲线
上，
，
(Ⅰ)
①
，
，
，
，
(Ⅱ)，
联立(Ⅰ)(Ⅱ)解得：
，
，
；
②如图3，
，
，
，
，
，
，
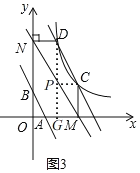
直线
的解析式为
(Ⅲ)，
双曲线
(Ⅳ)，
联立(Ⅲ)(Ⅳ)得：
，
即：
，
△
，
直线与双曲线
有唯一公共点，
△
，
△
，
(舍
或
，
，
．
故答案为：．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
