题目内容
15.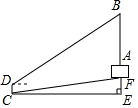 数学活动课上,老师和学生一起去侧量学校升旗台上旗杆AB的高度,如图,老师测得升旗台前斜坡FC的坡度为1:10(即EF:CE=1:10),学生吴昊站在离旗杆水平距离为27m(即CE=27m)的点C处,测得旗杆顶端B的仰角为30°,吴昊身高CD=1.6m,升旗台AF的高1.8m,请帮同学计算出旗杆AB的高度(结果精确到0.1米,$\sqrt{3}$≈1.73).
数学活动课上,老师和学生一起去侧量学校升旗台上旗杆AB的高度,如图,老师测得升旗台前斜坡FC的坡度为1:10(即EF:CE=1:10),学生吴昊站在离旗杆水平距离为27m(即CE=27m)的点C处,测得旗杆顶端B的仰角为30°,吴昊身高CD=1.6m,升旗台AF的高1.8m,请帮同学计算出旗杆AB的高度(结果精确到0.1米,$\sqrt{3}$≈1.73).
分析 如图作DG⊥BE于G,则四边形CDFE是矩形,DG=CE=27m,CD=GE=1.6m.在Rt△DBG中求出BG,再求出EF,根据AB=BG+GE-AE,即可解决问题.
解答 解:如图作DG⊥BE于G,则四边形CDFE是矩形,DG=CE=27m,CD=GE=1.6m.
在Rt△BDG中,∵∠DGB=90°,∠BDG=30°,DG=27,
∴BG=DG•tan30°=27×$\frac{\sqrt{3}}{3}$=9$\sqrt{3}$≈15.59m,
∵EF=$\frac{1}{10}$CE=2.7m,
∴AB=BE-AE=BG+GE-AE=15.59+1.6-2.7-1.8≈12.7m.
答:旗杆AB的高度为12.7m.
点评 本题考查解直角三角形的应用,坡度,仰角等知识,解题的关键是学会添加辅助线构造直角三角形,学会灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
10.下列抛物线顶点坐标为(-2,3)的是( )
| A. | y=-2(x+2)2+3 | B. | y=-3(x-2)2+3 | C. | y=-5(x+2)2-3 | D. | y=-5(x-2)2-3 |
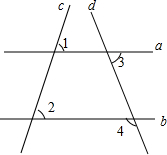 直线a,b,c,d的位置如图所示,已知∠1=58°,∠2=58°,∠3=70°,求∠4的度数.
直线a,b,c,d的位置如图所示,已知∠1=58°,∠2=58°,∠3=70°,求∠4的度数. 如图,在△ABC中,AD⊥BC,垂足为点D,∠C=2∠1,∠2=$\frac{3}{2}$∠1,求∠B的度数.
如图,在△ABC中,AD⊥BC,垂足为点D,∠C=2∠1,∠2=$\frac{3}{2}$∠1,求∠B的度数.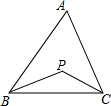 如图,△ABC,点P是∠B、∠C的平分线交点.
如图,△ABC,点P是∠B、∠C的平分线交点.