题目内容
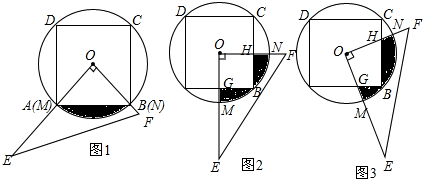
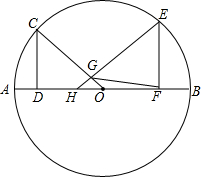已知AB是⊙O的直径，C、E是⊙O上的点，CD⊥AB，EF⊥AB，垂足分别为D、F，过点E作 EG⊥0C，垂足为G，延长EG交OA于H．求证：
（1）HO•HF=HG•HE；
（2）FG=CD．
考点：圆的综合题
专题：证明题
分析：（1）利用相似三角形的判定方法得出△HGO∽△HFE，进而得出即可；
（2）过点G作 GM⊥0H，垂足为M，连结OE，利用
=
，∠EHO=∠FHG得出△HGF∽△HOE，进而得出Rt△FGM∽Rt△EOG，即可得出
=
由OE=OC得出答案．
（2）过点G作 GM⊥0H，垂足为M，连结OE，利用
| HO |
| HE |
| HG |
| HF |
| GF |
| OE |
| CD |
| OC |
解答：证明：
（1）∵EG⊥0C，EF⊥AB
∴∠HGO=∠HFE=90°
又∵∠GHO=∠FHE，
∴△HGO∽△HFE，
∴
=
，
即HO•HF=HG•HE；
（2）如图1，过点G作 GM⊥0H，垂足为M，连结OE
∵
=
，∠EHO=∠FHG
∴△HGF∽△HOE
∴∠HFG=∠HEO
∴Rt△FGM∽Rt△EOG
∴
=
又 GM∥CD，
∴
=
即
=
∴
=
由OE=OC，得GF=CD
方法二：如图2，延长CD交⊙O于点N，延长EF交⊙O于点L，延长EH交⊙O于点K，连接KL，
则KL=2GF，CN=2CD
∵∠HEL=∠AOC，
∴KL=CN，∴GF=CD
（1）∵EG⊥0C，EF⊥AB∴∠HGO=∠HFE=90°
又∵∠GHO=∠FHE，
∴△HGO∽△HFE，
∴
| HO |
| HE |
| HG |
| HF |
即HO•HF=HG•HE；
（2）如图1，过点G作 GM⊥0H，垂足为M，连结OE
∵
| HO |
| HE |
| HG |
| HF |
∴△HGF∽△HOE
∴∠HFG=∠HEO
∴Rt△FGM∽Rt△EOG
∴
| GM |
| OG |
| GF |
| OE |
又 GM∥CD，
∴
| GM |
| CD |
| OG |
| OC |
| GM |
| OG |
| CD |
| OC |
∴
| GF |
| OE |
| CD |
| OC |
方法二：如图2，延长CD交⊙O于点N，延长EF交⊙O于点L，延长EH交⊙O于点K，连接KL，
则KL=2GF，CN=2CD
∵∠HEL=∠AOC，
∴KL=CN，∴GF=CD
点评：此题主要考查了圆的综合以及相似三角形的判定与性质，得出Rt△FGM∽Rt△EOG是解题关键．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
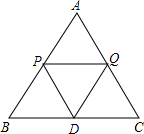如图，正三角形ABC中，P、Q分别为AB、AC边上的点，将△ABC沿PQ折叠，点A的对称点是点D，小明在研究此折叠问题时，发现一个有趣的结论：不论如何折叠，直线PD和直线BC所成的角总是等于DQ和AC所成的角．如图，点D恰好落在边BC上，试证明∠BDP=∠CQD．
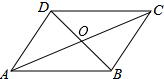如图，在四边形ABCD中，BC=12，OA=OC=13，BD=10，∠CBD=90°，求证：四边形ABCD为平行四边形．