题目内容
13.计算:(2+1)(22+1)(24+1)
=(2-1)(2+1)(22+1)(24+1)
=(22-1)(22+1)(24+1)
=(24-1)(24+1)
=(28-1)
根据上式的计算方法,请计算(3+1)(32+1)(34+1)…(332+1)-$\frac{{3}^{64}}{2}$的值.
分析 原式变形后,利用平方差公式计算即可得到结果.
解答 解:原式=$\frac{(3-1)(3+1)({3}^{2}+1)…({3}^{32}+1)-{3}^{64}}{2}$=$\frac{{3}^{64}-1-{3}^{64}}{2}$=-$\frac{1}{2}$.
点评 此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
3.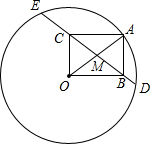 如图,⊙O的半径为20,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=12.延长BC,与⊙O分别交于D,E两点,则CE-BD的值等于( )
如图,⊙O的半径为20,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=12.延长BC,与⊙O分别交于D,E两点,则CE-BD的值等于( )
 如图,⊙O的半径为20,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=12.延长BC,与⊙O分别交于D,E两点,则CE-BD的值等于( )
如图,⊙O的半径为20,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=12.延长BC,与⊙O分别交于D,E两点,则CE-BD的值等于( )| A. | $\frac{24}{5}$ | B. | $\frac{28}{5}$ | C. | $\frac{36}{5}$ | D. | $\frac{48}{5}$ |
1. 如图,直线a∥b,直线c与a,b相交,∠1=50°,则∠2的度数为( )
如图,直线a∥b,直线c与a,b相交,∠1=50°,则∠2的度数为( )
 如图,直线a∥b,直线c与a,b相交,∠1=50°,则∠2的度数为( )
如图,直线a∥b,直线c与a,b相交,∠1=50°,则∠2的度数为( )| A. | 40° | B. | 50° | C. | 120° | D. | 130° |
8.下列各式计算正确的是( )
| A. | 2a+2=3a2 | B. | (-b2)3=-b5 | C. | a2•a3=a5 | D. | (m-n)2=m2-n2 |
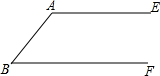 如图,AE∥BF,先按(1)的要求作图,再按(2)的要求证明
如图,AE∥BF,先按(1)的要求作图,再按(2)的要求证明 如图,正方形ABCD和正方形CEFG中,点D在CG上,已知:BC=1,CE=7,H是AF的中点,则AF=10,CH=5.
如图,正方形ABCD和正方形CEFG中,点D在CG上,已知:BC=1,CE=7,H是AF的中点,则AF=10,CH=5.