��Ŀ����
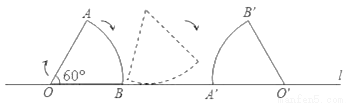
��ͼ�����뾶Ϊ2��Բ�Ľ�Ϊ60�������ֽƬAOB����ֱ��l�������������Ĺ���������A��O��B�䴦����O������·���ܳ�Ϊ_____��
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
��ͼ�����뾶Ϊ2��Բ�Ľ�Ϊ60�������ֽƬAOB����ֱ��l�������������Ĺ���������A��O��B�䴦����O������·���ܳ�Ϊ_____��
