Question

11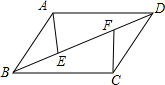．如图所示，点E，F是平行四边形ABCD对角线BD上的点，BF=DE，求证：AE=CF．

Answer 1

分析 根据平行四边形的性质可得AD∥BC，AD=BC，根据平行线的性质可得∠EDA=∠FBC，再加上条件ED=BF可利用SAS判定△AED≌△CFB，进而可得AE=CF．

解答 证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∴∠EDA=∠FBC，
在△AED和△CFB中，
$\left\{\begin{array}{l}{AD=BC}&{\;}\\{∠ADE=∠CBF}&{\;}\\{BF=DE}&{\;}\end{array}\right.$，
∴△AED≌△CFB（SAS），
∴AE=CF．

点评 此题主要考查了平行四边形的性质和全等三角形的判定和性质，关键是掌握平行四边形对边平行且相等．